Question

If ABCDEF is a regular hexagon and if $\overline{AB}+\overline{AC}+\overline{AD}+\overline{AE}+\overline{AF}=\lambda \overline{AD}$ , then $\lambda $ is:
(A). 0
(B). 1
(C). 2
(D). 3

Answer 1

Hint: We will be using the concepts of vector algebra. We will be using vector addition through triangle law of vector addition in which two vectors to be added is represented as the side of a triangle and resultant vector is the third side of the triangle.

Complete step-by-step solution -
We have been given a regular hexagon ABCDEF as

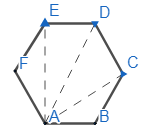
Now, we have been given that $\overline{AB}+\overline{AC}+\overline{AD}+\overline{AE}+\overline{AF}=\lambda \overline{AD}$. And we have to find the value of $\lambda $.
Now we know that according to the triangle law of vector addition, when two vectors are represented as two sides of a triangle with the order and magnitude then the third side is the resultant vector.
Now, we consider \[\Delta ACD\]. We get,
\[\overline{AC}+\overline{CD}=\overline{AD}\] …………………….. (1)
In $\Delta ADE$ we get $\overline{AE}+\overline{ED}=\overline{AD}$ …………………. (2)
Now, we will add (1) and (2)
\[\overline{AC}+\overline{CD}+\overline{AE}+\overline{ED}=2\overline{AD}\]……………….. (3)
Now, we know that ABCEDF is a regular hexagon, therefore, opposite sides are equal in magnitude and direction. Therefore,
$\overline{AF}=\overline{CD}$ …………… (4)
$\overline{ED}=\overline{AB}$ …………… (5)
Now we will substitute the value of $\overline{CD}$ and $\overline{ED}$ from (1) and (2) in (3) so that,
$\overline{AC}+\overline{AF}+\overline{AE}+\overline{AB}=2\overline{AD}$ .
Now, we will add $\overline{AD}$ on both sides. Therefore we have,
\[\overline{AB}+\overline{AC}+\overline{AD}+\overline{AE}+\overline{AF}=3\overline{AD}\].
Now, we will compare this with
$\overline{AB}+\overline{AC}+\overline{AD}+\overline{AE}+\overline{AF}=\lambda \overline{AD}$.
So, the value of $\lambda $ is 3.
Hence, the correct option is (D).

Note: To solve these types of questions one must know the triangle law of vector addition also it has to be noted that we have $\overline{AF}=\overline{CD}$ and $\overline{ED}=\overline{AD}$ through geometry. Here we need to know about the concept of vectors to be parallel.