Question

If $a,b,c$ denotes the lengths of the sides of a triangle opposite to angles $A,B,C$ respectively in $\Delta ABC$, then the correct relation among $a,b,c,A,B,C$ is given by which of the following option?
A) $(b + c)\sin (\dfrac{{B + C}}{2}) = a\cos \dfrac{A}{2}$
B) $(b - c)\cos \dfrac{A}{2} = a\sin (\dfrac{{B - C}}{2})$
C) $(b - c)\cos \dfrac{A}{2} = 2a\sin (\dfrac{{B - C}}{2})$
D) $(b - c)\sin (\dfrac{{B - C}}{2}) = a\cos \dfrac{A}{2}$

Answer 1

Hint:There is a trigonometric relation between sides and angles of a triangle. Using this relation and necessary trigonometric formulas, we can find the answer. Keep in mind angle sum of a triangle is $180^\circ $

Formula used:If $a,b,c$ denotes the sides of a triangle opposite to angles $A,B,C$ in $\Delta ABC$, then we have,
$\dfrac{a}{{\sin A}} = \dfrac{b}{{\sin B}} = \dfrac{c}{{\sin C}} = k$, for some value $k$.
For every angle $\theta $, we have,
$\cos (90 - \theta ) = \sin \theta $
$\sin 2\theta = 2\sin \theta \cos \theta $
For every $x,y$ ,
$\sin x - \sin y = 2\cos \dfrac{{x + y}}{2}\sin \dfrac{{x - y}}{2}$
Sum of the angles in a triangle is $180^\circ $.

Complete step-by-step answer:

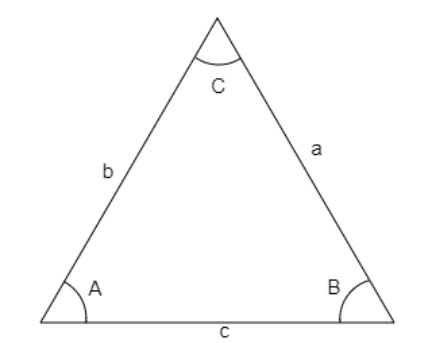
Given $a,b,c$ denotes the sides of a triangle opposite to angles $A,B,C$ in $\Delta ABC$,
then we have,
$\dfrac{a}{{\sin A}} = \dfrac{b}{{\sin B}} = \dfrac{c}{{\sin C}} = k$, for some value $k$.
$ \Rightarrow a = k\sin A,b = k\sin B,c = k\sin C$
Consider $\dfrac{{b - c}}{a}$
$ \Rightarrow \dfrac{{b - c}}{a} = \dfrac{{k\sin B - k\sin C}}{{k\sin A}} = \dfrac{{k(\sin B - \sin A)}}{{k\sin A}}$
Cancelling $k$ from numerator and denominator we have,
$ \Rightarrow \dfrac{{b - c}}{a} = \dfrac{{\sin B - \sin C}}{{\sin A}}$
For every $x,y$ ,
$\sin x - \sin y = 2\cos \dfrac{{x + y}}{2}\sin \dfrac{{x - y}}{2}$
Also, for every angle $\theta $, we have,
$\sin 2\theta = 2\sin \theta \cos \theta $
Using these relations, we get,
$ \Rightarrow \dfrac{{b - c}}{a} = \dfrac{{\sin B - \sin C}}{{\sin A}} = \dfrac{{2\cos \dfrac{{B + C}}{2}\sin \dfrac{{B - C}}{2}}}{{2\sin \dfrac{A}{2}\cos \dfrac{A}{2}}}$
Cancelling $2$ from numerator and denominator we have,
$ \Rightarrow \dfrac{{b - c}}{a} = \dfrac{{\cos \dfrac{{B + C}}{2}\sin \dfrac{{B - C}}{2}}}{{\sin \dfrac{A}{2}\cos \dfrac{A}{2}}} - - - (i)$
Now consider $\vartriangle ABC$. Here $A,B,C$ are the three angles.
$ \Rightarrow A + B + C = 180$
Rearranging the terms, we get,
$ \Rightarrow B + C = 180 - A$
Dividing both sides by $2$ we have,
$ \Rightarrow \dfrac{{B + C}}{2} = \dfrac{{180 - A}}{2} = 90 - \dfrac{A}{2}$
$ \Rightarrow \cos (\dfrac{{B + C}}{2}) = \cos (90 - \dfrac{A}{2})$
But $\cos (90 - \theta ) = \sin \theta $
$ \Rightarrow \cos (\dfrac{{B + C}}{2}) = \sin \dfrac{A}{2}$
Substituting this in $(i)$ we get,
$ \Rightarrow \dfrac{{b - c}}{a} = \dfrac{{\sin \dfrac{A}{2}\sin \dfrac{{B - C}}{2}}}{{\sin \dfrac{A}{2}\cos \dfrac{A}{2}}}$
Cancelling $\sin \dfrac{A}{2}$ from numerator and denominator we have,
$ \Rightarrow \dfrac{{b - c}}{a} = \dfrac{{\sin \dfrac{{B - C}}{2}}}{{\cos \dfrac{A}{2}}}$
Cross multiplying, we get,
$ \Rightarrow (b - c)\cos \dfrac{A}{2} = a\sin \dfrac{{B - C}}{2}$

So, the correct answer is “Option B”.

Note:Here we considered $\dfrac{{b - c}}{a}$ by looking into the options. Since there is no further clue from the question it is advisable to check the options and thus solve the answer. Further simplification should be done accordingly to reach the answer.AND remember important trigonometric formulas and identities for solving these types of problems.