Question

If AB=12cm, BC=16cm and AB is perpendicular to BC, then the radius of the circle passing through the points A, B and C is
A. 6cm
B. 8cm
C. 10cm
D. 20cm

Answer 1

Hint: Given that a triangle is inscribed inside a circle, this kind of circle is called the circumscribed circle. In geometry, the circumscribed circle or a circumcircle of a polygon is a circle that passes through all the vertices of the polygon. Here the polygon described is a triangle which is a three-sided polygon, and as given all its vertices are passing through the circumscribed circle.

Complete step by step answer:
Given it is a circumscribed circle, hence visualizing it as given below :
 

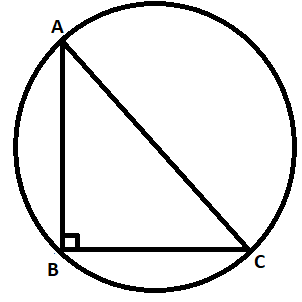
Given that the length of AB=12cm
Also given that the length of BC=16cm
All the vertices of the triangle ABC which are A, B and C are passing through the circumscribed circle.
The hypotenuse of the triangle ABC is the diameter of the circumscribed circle.
The hypotenuse of the triangle ABC is AC.
Thus the radius of the circle will be the half of the hypotenuse of the triangle ABC.
$\therefore $Radius of the circle = $\dfrac{{AC}}{2}$
As given that the triangle ABC is a right angled triangle.
Hence this triangle ABC should obey the Pythagoras theorem, which is given by:
$ \Rightarrow A{B^2} + B{C^2} = A{C^2}$
Finding the length of the hypotenuse AC, as given below:
$ \Rightarrow AB = 12$
$ \Rightarrow BC = 16$
Now substituting the values of $AB$ and $BC$ in the Pythagoras theorem, as given below:
$ \Rightarrow {(12)^2} + {(16)^2} = A{C^2}$
$ \Rightarrow A{C^2} = 144 + 256$
$ \Rightarrow A{C^2} = 400$
$ \Rightarrow AC = \sqrt {400} $
$\therefore AC = 20$cm
Hence the radius of the circle is the half of the hypotenuse AC, which is given by:
$ \Rightarrow $Radius of the circle = $\dfrac{{20}}{2}$cm
$\therefore $Radius of the circle = $10$cm

The radius of the circle passing through the points A, B and C is 10cm.

Note: Here as already discussed it is a circumscribed circle. The center of this circle is called the circumcenter and its radius is called the circumradius. It is very important to understand that the diameter and the hypotenuse are considered to be the same, i.e, here the hypotenuse of the triangle is the diameter of the circle.