Question

If a variable plane, at a distance of 3 units from the origin, intersects the coordinate axes at $A$, $B$ and $C$, then the locus of the centroid of $\Delta ABC$ is \[\]
A.$\dfrac{1}{{{x}^{2}}}+\dfrac{1}{{{y}^{2}}}+\dfrac{1}{{{z}^{2}}}=3$\[\]
B. $\dfrac{1}{{{x}^{2}}}+\dfrac{1}{{{y}^{2}}}+\dfrac{1}{{{z}^{2}}}=1$\[\]
C. $\dfrac{1}{{{x}^{2}}}+\dfrac{1}{{{y}^{2}}}+\dfrac{1}{{{z}^{2}}}=\dfrac{1}{9}$\[\]
D. $\dfrac{1}{{{x}^{2}}}+\dfrac{1}{{{y}^{2}}}+\dfrac{1}{{{z}^{2}}}=9$\[\]

Answer 1

Use the formula of the distance between a point and a plane to find out the value of ${{d}^{2}}$. Then find out the coordinates of $A$, $B$, and $C$ to use in the obtained equation. Finally, substitute variables for the equation of the loci.

Complete step-by-step solution:
The distance between a plane $ax+by+cz+d=0$ where $a,b,c,d$ are real numbers and a point $\left( {{x}_{0}},{{y}_{0}},{{z}_{0}} \right)$ in three dimension is given by the formula
\[r=\dfrac{\left| a{{x}_{0}}++b{{y}_{0}}+c{{z}_{0}}+d \right|}{{{\sqrt{{{a}^{2}}+{{b}^{2}}+c}}^{2}}}\]
The given equation of variable plane is $ax+by+cz+d=0$ and it also mentioned that distance between the plane from the origin is fixed 3 units wherever the plane moves in three dimension. The co-ordinates of the origin is $\left( 0,0,0 \right)$. Putting this in the plane to point distance formula
\[\begin{align}
  & 3=\dfrac{\left| a.0++b.0+c.0+d \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}} \\
 & \Rightarrow 3=\dfrac{\left| d \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}} \\
 & \Rightarrow d=9\left( {{a}^{2}}+{{b}^{2}}+{{c}^{2}} \right)...\left( 1 \right) \\
\end{align}\]

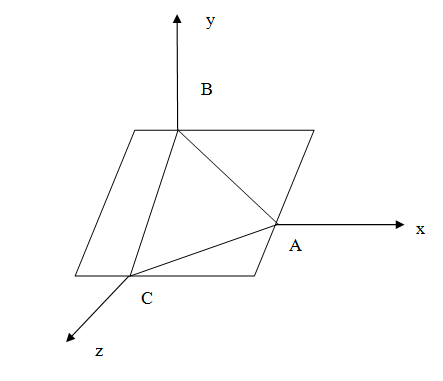
Let us assign $A$ as the point of intersection of the plane and $x$–axis , $B$ as the point of intersection of the plane and $y$–axis, $C$ as the point of intersection of the plane and $z$–axis.\[\]
In $x$–axis , $y=0$ and $z=0$ . Putting these in the equation of the plane , we find the co-ordinates $A$ as $\left( \dfrac{-d}{a},0,0 \right)$\[\]
In $y$–axis , $x=0$ and $z=0$ . Putting these in the equation of the plane, we find the co-ordinates $B$ as $\left( 0,\dfrac{-d}{b}.0 \right)$\[\]
In $z$–axis , $y=0$ and $x=0$ . Putting these in the equation of the plane, we find the co-ordinates $C$ as $\left( 0,0,\dfrac{-d}{c} \right)$\[\]
The centroid of any triangle whose vertices $\left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right),\left( {{x}_{2}},{{y}_{2}},{{z}_{2}} \right),\left( {{x}_{3}},{{y}_{3}},{{z}_{3}} \right)$ is given by the formula $\left( \dfrac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3},\dfrac{{{y}_{1}}+{{y}_{2}}+{{v}_{3}}}{3},\dfrac{{{z}_{1}}+{{z}_{2}}+{{z}_{3}}}{3} \right)$. So the centroid of the triangle $\Delta ABC$ is $\left( \dfrac{-d}{3a},\dfrac{-d}{3b},\dfrac{-d}{3c} \right)=\left( l,m,n \right)$. Now we observe the options given in the question and evaluate sum of inversed squares ,
\[\dfrac{1}{{{l}^{2}}}+\dfrac{1}{{{m}^{2}}}+\dfrac{1}{{{n}^{2}}}=\dfrac{9\left( {{a}^{2}}+{{b}^{2}}+{{c}^{2}} \right)}{{{d}^{2}}}\]
We use the value of ${{d}^{2}}$ obtained in equation (1) to get
\[\dfrac{1}{{{l}^{2}}}+\dfrac{1}{{{m}^{2}}}+\dfrac{1}{{{n}^{2}}}=\dfrac{9\left( {{a}^{2}}+{{b}^{2}}+{{c}^{2}} \right)}{9\left( {{a}^{2}}+{{b}^{2}}+{{c}^{2}} \right)}=1\]
No we treat $\left( l,m,n \right)$ as any point of the formed locus to get ,
\[\dfrac{1}{{{x}^{2}}}+\dfrac{1}{{{y}^{2}}}+\dfrac{1}{{{z}^{2}}}=1\]
So the correct option is B.\[\]

Note: We need to be careful of two signs involved in the distance formula $r=\dfrac{a{{x}_{0}}++b{{y}_{0}}+c{{z}_{0}}+d}{\pm {{\sqrt{{{a}^{2}}+{{b}^{2}}+c}}^{2}}}$. We also need to be careful of confusion in formulas of the centroid$\left( \dfrac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3},\dfrac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3},\dfrac{{{z}_{1}}+{{z}_{2}}+{{z}_{3}}}{3} \right)$ , the incentre $\left( \dfrac{a{{x}_{1}}+b{{x}_{2}}+c{{x}_{3}}}{a+b+c},\dfrac{a{{y}_{1}}+b{{y}_{2}}+c{{y}_{3}}}{a+b+c},\dfrac{a{{z}_{1}}+b{{z}_{2}}+c{{z}_{3}}}{a+b+c} \right)$ and the circumcenter $\left( \dfrac{{{x}_{1}}\sin A+{{x}_{2}}\sin B+{{x}_{3}}\sin C}{\sin A+\sin B+\sin C},\dfrac{{{y}_{1}}\sin A+{{y}_{2}}\sin B+{{y}_{3}}\sin C}{\sin A+\sin B+\sin C},\dfrac{{{z}_{1}}\sin A+{{z}_{2}}\sin B+{{z}_{3}}\sin C}{\sin A+\sin B+\sin C} \right)$ of a triangle with length of the sides $a,b,c$ and angles $A,B,C$ which can be determined using slopes.