Question

If a transversal intersects two lines such that bisectors of a pair of corresponding angles are parallel, then prove that the two lines are parallel.

Answer 1

Hint: In this problem, first consider a line which intersects two lines at two points. From these two points, draw bisectors of the respective angle formed with the line. By using the property of bisectors, we prove two pairs of angles to be equal and corresponding. If their corresponding angle then the lines must be parallel. By using this methodology, we can prove our answer.

Complete step by step answer:
One helpful axiom for proving this result is “If a transversal intersects two lines such that a pair of corresponding angles is equal then the two lines are parallel to each other."
Consider the figure as shown below:

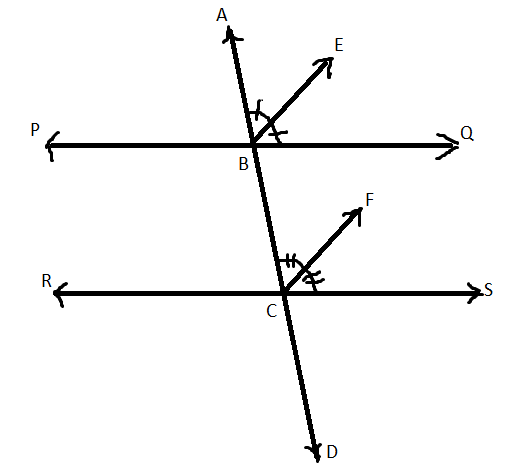
According to the figure, a transversal PQ intersects two lines AB and CD at respective points E and G. A set of two lines is produced from E and G. Line EF acts as a bisector to the angle $\angle PEB$ and the line GH acts a bisector to the angle $\angle EGD$.
Since, EF acts as a bisector to the angle $\angle PEB$:
$\angle PEF=\dfrac{1}{2}\angle PEB$
Also, line GH acts a bisector to the angle $\angle EGD$:
$\angle EGH=\dfrac{1}{2}\angle EGD$
Now, EF and GH are parallel and PQ act as a transversal line, therefore by corresponding angle theorem,
$\begin{align}
  & \angle PEF=\angle EGH \\
 & \therefore \dfrac{1}{2}\angle PEB=\dfrac{1}{2}\angle EGD \\
 & \angle PEB=\angle EGD \\
\end{align}$
So, the angles made by transversal and the original lines are also equal. So, they become the corresponding angles of a pair of lines.

Hence, again by using the converse of the corresponding angle axiom as stated at top, we conclude that lines AB and CD are parallel. Hence, our solution is proved.

Note: The key step for solving this problem is the knowledge of basic geometrical laws related to lines and transversal. The corresponding angle theorem plays a major role in solving the problem. Students must be also aware of the angle bisector concept. After having this much knowledge, the question is easily solved.