Question

If a line $y = 3x + 1$ cuts the parabola ${x^2} - 4x - 4y + 20 = 0$ at A and B, then the tangent of the angle subtended by line segment AB at origin is
A. $\dfrac{{8\sqrt 3 }}{{205}}$
B. $\dfrac{{8\sqrt 3 }}{{209}}$
C. $\dfrac{{8\sqrt 3 }}{{215}}$
D. None of these

Answer 1

Hint: In the given question $y = 3x + 1$ is the equation for line. Line is defined as a straight one-dimensional figure that ends infinitely in both the directions and is of no thickness. Also the given equation ${x^2} - 4x - 4y + 20 = 0$ is of parabola. Parabola is defined as a curve whose every point is at an equal distance from a fixed point, also known as the focus and a fixed straight line, also known as the directrix.

Complete step by step solution:
At first we will find the coordinates of point $A$ and point $B$. For this we will solve the equation of the straight line and the equation of the parabola, i.e. $y = 3x + 1$ and ${x^2} - 4x - 4y + 20 = 0$ respectively. Let us name them as
$y = 3x + 1$ {equation (1)}
${x^2} - 4x - 4y + 20 = 0$ {equation (2)}
From equation (1), we have $y = 3x + 1$. We will put this value of $y$ in equation (2) such that it becomes
$ \Rightarrow {x^2} - 4x - 4y + 20 = 0$
$ \Rightarrow {x^2} - 4x - 4(3x + 1) + 20 = 0$
On simplifying further, we get
$ \Rightarrow {x^2} - 4x - 12x - 4 + 20 = 0$
$ \Rightarrow {x^2} - 16x + 16 = 0$
On using the quadratic formula i.e $x = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}}$, we will get
$ \Rightarrow x = \dfrac{{ - ( - 16) + \sqrt {{{( - 16)}^2} - 4 \times 1 \times 16} }}{{2 \times 1}}$ or $ \Rightarrow x = \dfrac{{ - ( - 16) - \sqrt {{{( - 16)}^2} - 4 \times 1 \times 16} }}{{2 \times 1}}$
On simplifying the expression under the square root, we will get
$ \Rightarrow x = \dfrac{{16 + \sqrt {256 - 64} }}{2}$ or $ \Rightarrow x = \dfrac{{16 - \sqrt {256 - 64} }}{2}$
$ \Rightarrow x = \dfrac{{16 + \sqrt {192} }}{2}$ or $ \Rightarrow x = \dfrac{{16 - \sqrt {192} }}{2}$
On substituting the value of $\sqrt {192} = 8\sqrt 3 $, we will get
$ \Rightarrow x = \dfrac{{16 + 8\sqrt 3 }}{2}$ or $ \Rightarrow x = \dfrac{{16 - 8\sqrt 3 }}{2}$
$ \Rightarrow x = 8 + 4\sqrt 3 $ or $ \Rightarrow x = 8 - 4\sqrt 3 $
Since, we have two values of $x$ therefore we will find two values of $y$ by putting each value of $x$ in equation (1).
For $x = 8 + 4\sqrt 3 $, we have
$ \Rightarrow y = 3x + 1$
$ \Rightarrow y = 3(8 + 4\sqrt 3 ) + 1$
On simplifying further, we get
$ \Rightarrow y = 24 + 12\sqrt 3 + 1$
$ \Rightarrow y = 25 + 12\sqrt 3 $
So we have the coordinates of point $A$ as $(8 + 4\sqrt 3 ,25 + 12\sqrt 3 )$.
And for $x = 8 - 4\sqrt 3 $, we have
$ \Rightarrow y = 3x + 1$
$ \Rightarrow y = 3(8 - 4\sqrt 3 ) + 1$
On simplifying further, we get
$ \Rightarrow y = 24 - 12\sqrt 3 + 1$
$ \Rightarrow y = 25 - 12\sqrt 3 $
So we have the coordinates of point $B$ as $(8 - 4\sqrt 3 ,25 - 12\sqrt 3 )$.
As the question is that we have to find the tangent of the angle subtended by line segment AB at origin. The question can be understood more clearly by the figure given below:

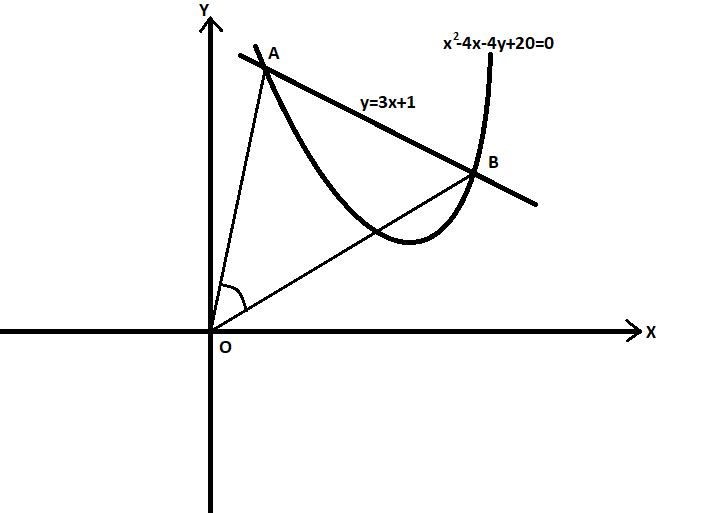
So from the figure, we get to know that we have to find the angle between line AO and line BO. But for this, we will have to find the equations for these lines.
Hence, we will use the two-point method to form the equation of the line. It states that if two points $P({x_1},{y_1})$ and $Q({x_2},{y_2})$ are given then the equation for the line $PQ$ can be given as
$(y - {y_1}) = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}(x - {x_1})$
For the line $OA$, we have $O(0,0)$ and $A(8 + 4\sqrt 3 ,25 + 12\sqrt 3 )$. Hence the equation of $OA$ will be
$ \Rightarrow (y - 0) = \dfrac{{(25 + 12\sqrt 3 ) - 0}}{{(8 + 4\sqrt 3 ) - 0}}(x - 0)$
$ \Rightarrow y = \dfrac{{25 + 12\sqrt 3 }}{{8 + 4\sqrt 3 }}x$
Since the denominator contains a complex number therefore we will have to rationalize it, such that
$ \Rightarrow y = (\dfrac{{25 + 12\sqrt 3 }}{{8 + 4\sqrt 3 }} \times \dfrac{{8 - 4\sqrt 3 }}{{8 - 4\sqrt 3 }})x$
$ \Rightarrow y = \dfrac{{(25 + 12\sqrt 3 )(8 - 4\sqrt 3 )}}{{(8 + 4\sqrt 3 )(8 - 4\sqrt 3 )}}x$
On multiplying both the expression together in the numerator and denominator, we will get
$ \Rightarrow y = \{ \dfrac{{200 + 96\sqrt 3 - 100\sqrt 3 - 144}}{{{{(8)}^2} - {{(4\sqrt 3 )}^2}}}\} x$
$ \Rightarrow y = (\dfrac{{56 - 4\sqrt 3 }}{{64 - 48}})x$
On simplifying the denominator further, we get
$ \Rightarrow y = \dfrac{{56 - 4\sqrt 3 }}{{16}}x$
$ \Rightarrow y = \dfrac{{14 - \sqrt 3 }}{4}x$
Hence, we have the equation for line $OA$ as $y = \dfrac{{14 - \sqrt 3 }}{4}x$.
For the line $OB$, we have $O(0,0)$ and $A(8 - 4\sqrt 3 ,25 - 12\sqrt 3 )$. Hence the equation of $OB$ will be
$ \Rightarrow (y - 0) = \dfrac{{(25 - 12\sqrt 3 ) - 0}}{{(8 - 4\sqrt 3 ) - 0}}(x - 0)$
$ \Rightarrow y = \dfrac{{25 - 12\sqrt 3 }}{{8 - 4\sqrt 3 }}x$
Since the denominator contains a complex number therefore we will have to rationalize it, such that
$ \Rightarrow y = (\dfrac{{25 - 12\sqrt 3 }}{{8 - 4\sqrt 3 }} \times \dfrac{{8 + 4\sqrt 3 }}{{8 + 4\sqrt 3 }})x$
$ \Rightarrow y = \dfrac{{(25 - 12\sqrt 3 )(8 + 4\sqrt 3 )}}{{(8 - 4\sqrt 3 )(8 + 4\sqrt 3 )}}x$
On multiplying both the expression together in the numerator and denominator, we will get
$ \Rightarrow y = \{ \dfrac{{200 + 100\sqrt 3 - 96\sqrt 3 - 144}}{{{{(8)}^2} - {{(4\sqrt 3 )}^2}}}\} x$
$ \Rightarrow y = (\dfrac{{56 + 4\sqrt 3 }}{{64 - 48}})x$
On simplifying the denominator further, we get
$ \Rightarrow y = \dfrac{{56 + 4\sqrt 3 }}{{16}}x$
$ \Rightarrow y = \dfrac{{14 + \sqrt 3 }}{4}x$
Hence, we have the equation for line $OB$ as $y = \dfrac{{14 + \sqrt 3 }}{4}x$.
Let us name the equations for line $OA$ and line $OB$ respectively as
$y = \dfrac{{14 - \sqrt 3 }}{4}x$ {equation (3)}
$y = \dfrac{{14 + \sqrt 3 }}{4}x$ {equation (4)}
The given equations are in the form of $y = mx$ where $m$ is known as the slope of the equation. So we have
${m_{OA}} = \dfrac{{14 - \sqrt 3 }}{4}$, and
${m_{OB}} = \dfrac{{14 + \sqrt 3 }}{4}$
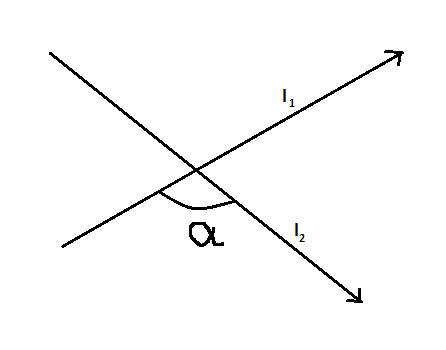
Now, it must be known that if there are two lines named ${l_1}$ and ${l_2}$ such that their slopes are ${m_1}$ and ${m_2}$ respectively, then the tangent of the angle between the two lines namely ${l_1}$ and ${l_2}$ can be given as
$\tan \alpha = |\dfrac{{{m_1} - {m_2}}}{{1 + {m_1}{m_2}}}|$

Now to find the tangent of the angle $\theta $ between line $OA$ and line $OB$ having slopes ${m_{OA}}$ and ${m_{OB}}$ respectively, we will apply the above given formula such that
$\tan \theta = |\dfrac{{{m_{OA}} - {m_{OB}}}}{{1 + {m_{OA}}{m_{OB}}}}|$
On substituting the required values, we will get
$ \Rightarrow \tan \theta = |\dfrac{{\dfrac{{14 - \sqrt 3 }}{4} - \dfrac{{14 + \sqrt 3 }}{4}}}{{1 + (\dfrac{{14 - \sqrt 3 }}{4})(\dfrac{{14 + \sqrt 3 }}{4})}}|$
$ \Rightarrow \tan \theta = |\dfrac{{\dfrac{{(14 - \sqrt 3 ) - (14 + \sqrt 3 )}}{4}}}{{1 + (\dfrac{{(14 - \sqrt 3 )(14 + \sqrt 3 )}}{{4 \times 4}})}}|$
On simplifying both the numerator and denominator further, we will get
$ \Rightarrow \tan \theta = |\dfrac{{\dfrac{{14 - \sqrt 3 - 14 - \sqrt 3 }}{4}}}{{1 + \dfrac{{{{(14)}^2} - {{(\sqrt 3 )}^2}}}{{16}}}}|$
$ \Rightarrow \tan \theta = |\dfrac{{\dfrac{{ - 2\sqrt 3 }}{4}}}{{1 + \dfrac{{196 - 3}}{{16}}}}|$
On further simplifying the fraction in the numerator and the denominator, we get
$ \Rightarrow \tan \theta = |\dfrac{{\dfrac{{ - 1\sqrt 3 }}{2}}}{{1 + \dfrac{{193}}{{16}}}}|$
$ \Rightarrow \tan \theta = |\dfrac{{\dfrac{{ - \sqrt 3 }}{2}}}{{\dfrac{{193 + 16}}{{16}}}}|$
On simplifying the denominator, we will get
$ \Rightarrow \tan \theta = |\dfrac{{\dfrac{{ - \sqrt 3 }}{2}}}{{\dfrac{{209}}{{16}}}}|$
$ \Rightarrow \tan \theta = |\dfrac{{ - \sqrt 3 }}{2} \times \dfrac{{16}}{{209}}|$
On simplifying the expression on the right hand side of the equation, we will get
$ \Rightarrow \tan \theta = |\dfrac{{ - 8\sqrt 3 }}{{209}}|$
On applying mod, we will get
$ \Rightarrow \tan \theta = \dfrac{{8\sqrt 3 }}{{209}}$
Since the tangent of angle between line $OA$ and line $OB$ is the tangent of angle subtended by line segment $AB$at origin.
Hence, tangent of the angle subtended by line segment $AB$at origin is $\dfrac{{8\sqrt 3 }}{{209}}$.

Therefore, the correct answer is option C.

Note:
It must be kept in mind that the tangent of the angle subtended by any line segment at origin is different from the slope of that line. Also the slope of the line is the tangent of the angle between the line and the positive x-axis in the anticlockwise direction.