Question

If a line intersects two concentric circles with centre A in points P, Q, R and S respectively, then prove that \[PQ = RS\].

Answer 1

Hint: First draw a figure reflecting all the points mentioned in the question then a perpendicular from center will bisect that chord Use this relation to get the required proof.

Complete Step by Step Solution:
Let us try to draw the figure of the concentric circles along with the line

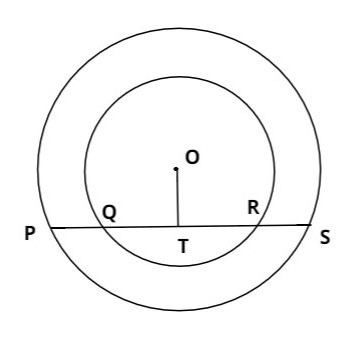
As we can see that QR is a Chord on the smaller circle and PS is the chord on the larger circle
Clearly at OT is the perpendicular on the chord and also bisects it
To Prove: \[PQ = RS\]
Proof:
Perpendicular from the center of the circle bisects the chord
\[\begin{array}{l}
QT = RT...........................(1)\\
PT = ST............................(2)
\end{array}\]
Now let us try to subtract them both and lets see what we get
Subtracting Equation (1) from equation (2) We get,
\[PT - QT = ST - RT\]
From the figure it is very much clear that
\[\begin{array}{l}
PT - QT = PQ\\
ST - RT = RS\\
\therefore PQ = RS (proved)
\end{array}\]

Note: Drawing the figure correctly was very much important as if we had interchanged the position for P and R the outcome would be completely different also note that the theorem that any perpendicular from the center of the circle bisects the chord.