Question

If a > b > 0, then the minimum value of $a\sec \theta -b\tan \theta \ \forall \theta \in \left( 0,\dfrac{\pi }{2} \right)$
(a) $\sqrt{{{a}^{2}}-{{b}^{2}}}$
(b) a – b
(c) $\sqrt{a-b}$
(d) ${{\left( {{a}^{2}}-{{b}^{2}} \right)}^{\dfrac{3}{2}}}$

Answer 1

Hint: To find the minimum of any expression, we need to derivate the expression once with respect to the variable of the expression and equate it to zero. Then we will find the value of the variable and substitute the variable in the original expression. This will give us the minimum or maximum of the expression. We need to keep in mind that derivative sec x is sec x tan x and tan x is ${{\sec }^{2}}\text{x}$.

Complete step-by-step answer:
The expression given to us is $a\sec \theta -b\tan \theta \ \forall \theta \in \left( 0,\dfrac{\pi }{2} \right)$ and we also know that a > b > 0.
So, let $f\left( \theta \right)=a\sec \theta -b\tan \theta $.
Now, to find the extreme values, we will derivate this $f\left( \theta \right)$ once and equate it to 0.
We know that derivative sec x is sec x tan x and tan x is ${{\sec }^{2}}\text{x}$.
Thus $f'\left( \theta \right)=a\sec \theta \tan \theta -b{{\sec }^{2}}\theta $
We shall now substitute $f'\left( \theta \right)=0$.
$\Rightarrow a\sec \theta \tan \theta -b{{\sec }^{2}}\theta =0$
It is evident that we can take $\sec \theta $ as common.
$\Rightarrow \sec \theta \left( a\tan \theta -b\sec \theta \right)=0$
Now, either $\sec \theta $ = 0 or $a\tan \theta -b\sec \theta $ = 0.
But $\sec \theta $ is never 0.
Thus, we know that $a\tan \theta -b\sec \theta $ = 0
$\begin{align}
  & \Rightarrow a\tan \theta =b\sec \theta \\
 & \Rightarrow \sin \theta =\dfrac{b}{a} \\
\end{align}$
This means in a right angled triangle, opp = b and hyp = a, thus adj = $\sqrt{{{a}^{2}}-{{b}^{2}}}$.

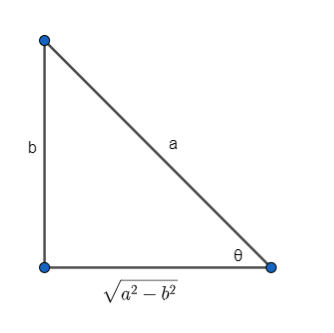
$\begin{align}
  & \Rightarrow \tan \theta =\dfrac{b}{\sqrt{{{a}^{2}}-{{b}^{2}}}} \\
 & \Rightarrow \sec \theta =\dfrac{a}{\sqrt{{{a}^{2}}-{{b}^{2}}}} \\
\end{align}$
Thus, if we shall substitute $\tan \theta =\dfrac{b}{\sqrt{{{a}^{2}}-{{b}^{2}}}}$ and $\sec \theta =\dfrac{a}{\sqrt{{{a}^{2}}-{{b}^{2}}}}$ in the original expression $a\sec \theta -b\tan \theta $.
$\begin{align}
  & \Rightarrow a\left( \dfrac{a}{\sqrt{{{a}^{2}}-{{b}^{2}}}} \right)-b\left( \dfrac{b}{\sqrt{{{a}^{2}}-{{b}^{2}}}} \right) \\
 & \Rightarrow \dfrac{{{a}^{2}}}{\sqrt{{{a}^{2}}-{{b}^{2}}}}-\dfrac{{{b}^{2}}}{\sqrt{{{a}^{2}}-{{b}^{2}}}} \\
\end{align}$
As the denominator is equal, we can carry the operation in the numerator.
$\Rightarrow \dfrac{{{a}^{2}}-{{b}^{2}}}{\sqrt{{{a}^{2}}-{{b}^{2}}}}$
We shall now rationalise the denominator. To rationalise we will multiply and divide the resultant expression by $\sqrt{{{a}^{2}}-{{b}^{2}}}$.
$\Rightarrow \dfrac{{{a}^{2}}-{{b}^{2}}}{\sqrt{{{a}^{2}}-{{b}^{2}}}}\times \dfrac{\sqrt{{{a}^{2}}-{{b}^{2}}}}{\sqrt{{{a}^{2}}-{{b}^{2}}}}$
We know that the product of $\sqrt{{{a}^{2}}-{{b}^{2}}}$ and $\sqrt{{{a}^{2}}-{{b}^{2}}}$ is ${{a}^{2}}-{{b}^{2}}$. ${{a}^{2}}-{{b}^{2}}$ in the numerator and ${{a}^{2}}-{{b}^{2}}$ in the denominator cancels out.
$\begin{align}
  & \Rightarrow \dfrac{\left( {{a}^{2}}-{{b}^{2}} \right)\sqrt{{{a}^{2}}-{{b}^{2}}}}{\left( {{a}^{2}}-{{b}^{2}} \right)} \\
 & \Rightarrow \sqrt{{{a}^{2}}-{{b}^{2}}} \\
\end{align}$
Therefore, the minimum value of $a\sec \theta -b\tan \theta \ \forall \theta \in \left( 0,\dfrac{\pi }{2} \right)$ is $\sqrt{{{a}^{2}}-{{b}^{2}}}$
Hence, option (a) is the correct option.

Note: Derivation of any expression yields extreme values of the expression. It can be minimum or maximum or sometimes we can get both, if we can factorise the derived expression. In the case we get two values of the variable, we need to substitute the variables one by one to get maximum and minimum.