Question

If \[a\] and \[b\] are two non collinear vectors and \[x,y\] are two scalars such that \[\overrightarrow a x + \overrightarrow b y = 0\] this implies that:
A. \[x = y = - 1\]
B. \[x = y = 0\]
C. \[x = y = 1\]
D. \[x = y = i\]

Answer 1

Hint: In this question, we will go for option verification and find out for which values of \[x,y\] the given two vectors \[a\] and \[b\]are non-collinear. So, use this concept to reach the solution of the given problem.

Complete step-by-step answer:
Given \[a\] and \[b\] are two non-collinear vectors and \[x,y\] are two scalars.
Also, \[\overrightarrow a x + \overrightarrow b y = 0\]
That implies \[\overrightarrow a = - \dfrac{y}{x}\overrightarrow b ..................................\left( 1 \right)\]
If \[x\] and \[y\] are non-zero, then the two vectors \[a\] and \[b\] are collinear, because \[\overrightarrow a = \lambda \overrightarrow b \] where \[\lambda \] is scalar as shown in the below figure:

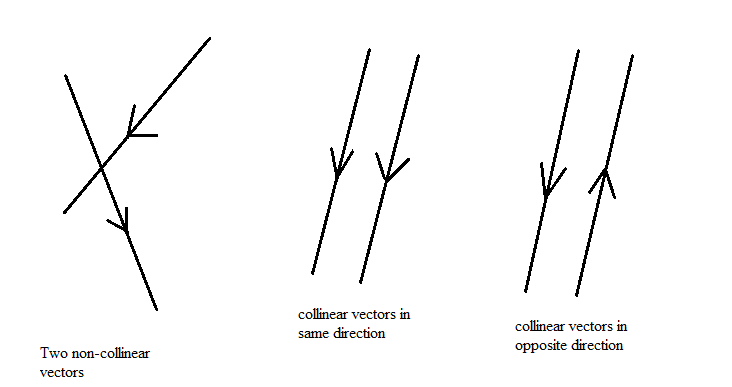
Now, we will go for the option verification to check whether the two vectors \[a\] and \[b\] are collinear or not.
A. By substituting \[x = y = - 1\] in equation (1), we have
\[
   \Rightarrow \overrightarrow a = - \dfrac{{ - 1}}{{ - 1}}\overrightarrow b \\
  \therefore \overrightarrow a = - \overrightarrow b \\
\]
which is of the form \[\overrightarrow a = \lambda \overrightarrow b \]. So, for the values of \[x = y = - 1\], \[a\] and \[b\] are collinear vectors.
B. By substituting \[x = y = 0\] in equation (1), we have
\[ \Rightarrow \overrightarrow a = - \dfrac{0}{0}\overrightarrow b \]
which is an indeterminate form. So, for the values of \[x = y = 0\], \[a\] and \[b\] are non-collinear vectors.
C. By substituting \[x = y = 1\] in equation (1), we have
\[
   \Rightarrow \overrightarrow a = - \dfrac{1}{1}\overrightarrow b \\
  \therefore \overrightarrow a = - \overrightarrow b \\
\]
which is of the form \[\overrightarrow a = \lambda \overrightarrow b \]. So, for the values of \[x = y = 1\], \[a\] and \[b\] are collinear vectors.
D. By substituting \[x = y = i\] in equation (1), we have
\[
   \Rightarrow \overrightarrow a = - \dfrac{i}{i}\overrightarrow b \\
  \therefore \overrightarrow a = - \overrightarrow b \\
\]
which is of the form \[\overrightarrow a = \lambda \overrightarrow b \]. So, for the values of \[x = y = i\], \[a\] and \[b\] are collinear vectors.
Therefore, only for the values of \[x = y = 0\], the two vectors \[a\] and \[b\] are collinear.
Thus, the correct option is B. \[x = y = 0\]

So, the correct answer is “Option B”.

Note: We can use any of the given conditions to prove the collinearity for two vectors:
1. Two vectors \[a\] and \[b\] are collinear if there exists a number \[n\] such that \[\overrightarrow a = n\overrightarrow b \].
2. Two vectors are collinear if relations of their coordinates are equal.
3. Two vectors are collinear if their cross product is equal to the zero vector.