Question

If $25$ people applied for programme A, $50$ people for programme B, $10$ people for both. So find the number of employees applied only for A.

Answer 1

Hint: This question is related to basic concepts of set theory. Here we are given 2 programmes and number of persons applied for each programme respectively. We have to find the number of persons who applied for programme A.

Complete step-by-step answer:
So, we have two programmes A and B.
Number of people applied for programme A $ = n\left( A \right) = 25$
Number of people applied for programme B $ = n\left( B \right) = 50$
We are also given the number of people that have applied for both the programmes. We also know that intersection of two sets A and B represents the events that are common to both the sets.
Now, number of people applied for both the programmes $ = n\left( {A \cap B} \right) = 10$
Now, we have to find the number of persons that applied for programme A only which are given by subtracting the number of persons applied for both programmes from number of persons who applied for programme A, these are denoted by $n\left( {only\,A} \right)$.
We will visualise the situation diagrammatically as below.

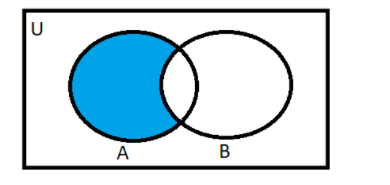
\[n\left( {only\,A} \right) = n\left( A \right) - n\left( {A \cap B} \right)\]
Substituting the values of $n\left( A \right)$ and $n\left( {A \cap B} \right)$, we get,
\[ \Rightarrow n\left( {only\,A} \right) = 25 - 10\]
\[ \Rightarrow n\left( {only\,A} \right) = 15\]
Hence, the number of people that applied only for the programme A is $15$.
So, the correct answer is “15”.

Note: The main thing to keep in mind while doing this question is the basic concepts of set theory and basic formulas which are applied directly, that is, \[n\left( {only\,A} \right) = n\left( A \right) - n\left( {A \cap B} \right)\]. Take care while doing the calculations. Keep in mind other formulas such as $n\left( {A \cup B} \right) = n\left( A \right) + n\left( B \right) - n\left( {A \cap B} \right)$ to solve many other such questions.