Question

How do you identify if the equation \[9{{x}^{2}}+4{{y}^{2}}-36=0\] is a parabola, ellipse, or hyperbola and how do you graph it?

Answer 1

Hint: The general equation of a conic is \[a{{x}^{2}}+b{{y}^{2}}+2hxy+2gx+2fy+c=0\]. We can determine whether the given conic is a circle, ellipse, or hyperbola from the equation of the conic. For the conic of the equation \[a{{x}^{2}}+b{{y}^{2}}+2hxy+2gx+2fy+c=0\],
If \[a=b\And h=0\], then the conic is a circle. If \[\Delta =4({{h}^{2}}-ab)\] is negative, then the conic is an ellipse. If the \[\Delta =4({{h}^{2}}-ab)\] is positive then the conic is a hyperbola.

Complete step by step answer:
The given equation of conic is \[9{{x}^{2}}+4{{y}^{2}}-36=0\]. Comparing with the general equation of the conic \[a{{x}^{2}}+b{{y}^{2}}+2hxy+2gx+2fy+c=0\], we get \[a=9,b=4,c=-36,\And h=g=f=0\].
Let’s verify the conditions for the circle, ellipse, and hyperbola.
Here as \[a\ne b\] the conic of the equation is not a circle.
\[\Delta =4({{h}^{2}}-ab)\], substituting the value of coefficients, we get
\[\begin{align}
  & \Rightarrow \Delta =4\left( {{0}^{2}}-9\times 4 \right) \\
 & \Rightarrow \Delta =4\left( -36 \right) \\
\end{align}\]
Multiplying 4 and \[-36\] equals \[-144\], substituting above we get
\[\Rightarrow \Delta =-144\]
Hence, as \[\Delta \] is a negative value the equation is of an ellipse.
To graph the ellipse, we first have to rearrange the given equation, as follows
\[9{{x}^{2}}+4{{y}^{2}}-36=0\]
Adding 36 to both sides of the equation, we get
\[\Rightarrow 9{{x}^{2}}+4{{y}^{2}}-36+36=0+36\]
\[\Rightarrow 9{{x}^{2}}+4{{y}^{2}}=36\]
Dividing both sides of the above equation by 36, we get
\[\Rightarrow \dfrac{9{{x}^{2}}+4{{y}^{2}}}{36}=\dfrac{36}{36}\]
The above equation can also be written as
\[\Rightarrow \dfrac{9{{x}^{2}}}{36}+\dfrac{4{{y}^{2}}}{36}=1\]
Canceling out common factors from the left-hand side of the equation, we get
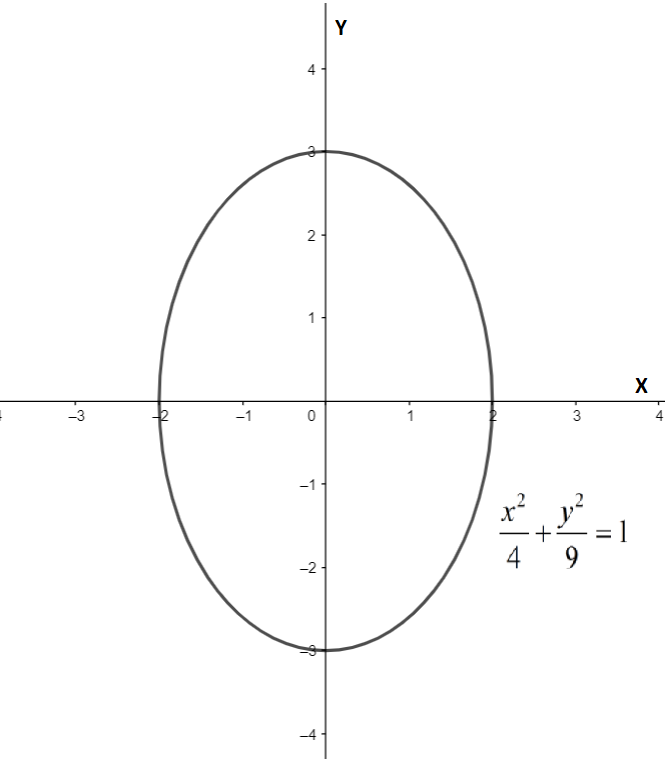
\[\Rightarrow \dfrac{{{x}^{2}}}{4}+\dfrac{{{y}^{2}}}{9}=1\]
We can graph the ellipse \[\dfrac{{{x}^{2}}}{4}+\dfrac{{{y}^{2}}}{9}=1\] as follows
 

Note:
To identify the conic from the equation, one should remember the different properties & conditions of the conics. One can make calculation mistakes while finding the coefficient of the \[x,y\And xy\]. It should be remembered that in the general equation their coefficients are \[2g,2f\And 2h\] respectively. Hence, we have to half the coefficients of \[x,y\And xy\]to find the values of \[g,f\And h\] and then use them to verify conditions.