Question

Hypotenuse $AC$ of right triangle $ABC$ is divided into $3$ equal parts. Two line segments parallel to $CB$ are drawn from the points of division. If $BC=30cm$, then find the sum of lengths of the two drawn line segments?

Answer 1

Hint: Here, let us assume that, $AG=GE=EC=x$ and $BC\parallel DE\parallel GF$. Use BPT for $\Delta ABC$ and $BC\parallel DE$ and in $\Delta ABC$ and $BC\parallel FG$. After that add both.

Complete step-by-step answer:

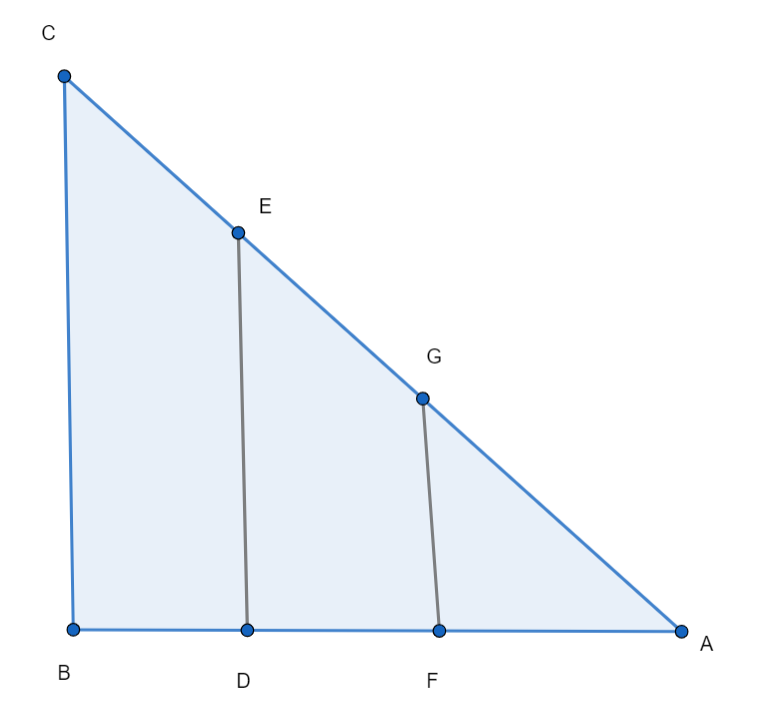
Here, let us assume that,
$AG=GE=EC=x$ …………. (1)
And also,
$BC\parallel DE\parallel GF$ ……………… (2)
We are given that, $BC=30cm$
Now using BPT,
BPT is, if a line is drawn parallel to one side of a triangle intersecting the other two sides in distinct points, then the other two sides are divided in the same ratio.
From BPT, in $\Delta ABC$ and $BC\parallel DE$,
$\dfrac{AE}{DE}=\dfrac{AC}{BC}$
We can see in figure that,
$AE=AG+GE$
Also, $AC=AG+GE+EC$
Now substituting values we get,
$\dfrac{AG+GE}{DE}=\dfrac{AG+GE+EC}{BC}$
Now from (1) and (2) we get,
$\Rightarrow$ $\dfrac{x+x}{DE}=\dfrac{x+x+x}{30}$
Now simplifying we get,
$\Rightarrow$ $\dfrac{2x}{DE}=\dfrac{3x}{30}$
$\Rightarrow$ $2=\dfrac{3DE}{30}$
Again, simplifying we get,
$\Rightarrow$ $DE=20cm$ …………… (3)
Similarly, From BPT, in $\Delta ABC$ and $BC\parallel FG$,
$\dfrac{AG}{FG}=\dfrac{AC}{BC}$
Now again substituting, $AC=AG+GE+EC$ in above equation we get,
$\dfrac{AG}{FG}=\dfrac{AG+GE+EC}{BC}$
From (1) and (2), we get,
$\Rightarrow$ $\dfrac{x}{FG}=\dfrac{x+x+x}{30}$
Now simplifying we get,
$\Rightarrow$ $\dfrac{x}{FG}=\dfrac{3x}{30}$
$\Rightarrow$ $\dfrac{1}{FG}=\dfrac{3}{30}$
$\Rightarrow$ $FG=10cm$ ………………. (4)
Now, adding (1) and (2), we get,
$\Rightarrow$ $DE+FG=20+10=30cm$
Therefore, the sum of lengths of two line segments is $30cm$.
Additional information:
In Geometry, a triangle is a three-sided polygon that consists of three edges and three vertices. The most important property of a triangle is that the sum of the internal angles of a triangle is equal to $180$ degrees. This property is called the angle sum property of triangles. Basic Proportionality theorem was introduced by a famous Greek Mathematician, Thales, hence it is also called Thales Theorem. According to him, for any two equiangular triangles, the ratio of any two corresponding sides is always the same.


Note: For any two equiangular triangles, the ratio of any two corresponding sides is always the same. Based on this concept, he gave the theorem of basic proportionality (BPT). This concept has been introduced in similar triangles. If two triangles are similar to each other then
i) Corresponding angles of both the triangles are equal
ii) Corresponding sides of both the triangles are in proportion to each other