Question

How do you solve \[\left| 1-2x \right|>10\]?

Answer 1

Hint: Substitute the expression inside the modulus sign equal to 0 and find the values of x. Now, represent these values on a number line and consider different intervals of x one by one. Find the sign of the function \[\left( 1-2x \right)\] in the intervals and accordingly remove the modulus sign to form a linear inequality and solve for the value of x. If \[\left( 1-2x \right)\] is negative then write \[\left| 1-2x \right|=-\left( 1-2x \right)\] and if \[\left( 1-2x \right)\] is positive in any interval then write \[\left| 1-2x \right|=\left( 1-2x \right)\].

Complete step by step solution:
Here, we have been provided with the inequality \[\left| 1-2x \right|>10\] and we are asked to solve it. That means we have to find the values of x or in other words, the interval of values of x.
Now, to solve the given inequality first we need to remove the modulus sign. To remove the modulus sign we need to check the sign of the expression inside the modulus. So, substituting the value of the expression \[\left( 1-2x \right)\] equal to 0, we get,
\[\begin{align}
  & \Rightarrow 1-2x=0 \\
 & \Rightarrow 2x=1 \\
 & \Rightarrow x=\dfrac{1}{2} \\
\end{align}\]
Representing this value of x on the number line, we have,

Here, we have two intervals they are: \[x\in \left( -\infty ,\dfrac{1}{2} \right)\] and \[x\in \left( \dfrac{1}{2},\infty \right)\]. So, we have to check the sign of the function \[\left( 1-2x \right)\] in these intervals one by one.
(i) When \[-\infty < x < \dfrac{1}{2}\]
In this case we have \[\left( 1-2x \right)\] positive, so by removing the modulus sign we get the inequality as: -
\[\begin{align}
  & \Rightarrow 1-2x > 10 \\
 & \Rightarrow -2x > 10-1 \\
 & \Rightarrow 2x < 9 \\
\end{align}\]
\[\begin{align}
  & \Rightarrow x < \dfrac{9}{2} \\
 & \Rightarrow -\infty < x < \dfrac{9}{2} \\
\end{align}\]
But we can see that we have the condition \[-\infty < x < \dfrac{1}{2}\]. So, we need to take the intersection of the two sets of values of x. Therefore, we have,

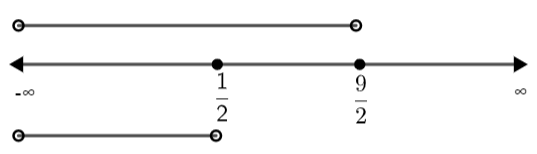
Clearly, the common value of x lies in the interval \[\left( -\infty ,\dfrac{1}{2} \right)\].
\[\Rightarrow x\in \left( -\infty ,\dfrac{1}{2} \right)\]
(ii) When \[\dfrac{1}{2}\le x < \infty \]
In this case \[\left( 1-2x \right)\] is negative, so removing the modulus sign and writing the inequality, we get,
\[\begin{align}
  & \Rightarrow -\left( 1-2x \right) > 10 \\
 & \Rightarrow 2x-1 > 10 \\
 & \Rightarrow 2x > 11 \\
 & \Rightarrow x > \dfrac{11}{2} \\
 & \Rightarrow \dfrac{11}{2} < x < \infty \\
\end{align}\]
But here the condition \[\dfrac{1}{2}\le x < \infty \], so in this case also we have to take the intersection of the two sets of values of x. Therefore, we have,

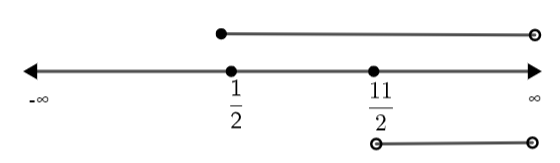
Clearly, the common value of x lies in the interval \[\left( \dfrac{11}{2},\infty \right)\].
\[\Rightarrow x\in \left( \dfrac{11}{2},\infty \right)\]
Since, both the cases are possible so the final values of x obtained in each case can be considered as the solution set. For this we need to take the intersection of the two sets of values of x.

Hence, the solution set of the given inequality can be given as: - \[x\in \left( -\infty ,\dfrac{1}{2} \right)\cup \left( \dfrac{11}{2},\infty \right)\].

Note: One must remember the steps that we have followed to solve the above inequality. You may also remember the direct formulas of two basic inequalities containing the modulus function given as: - if \[\left| x \right|\le a\] then \[-a\le x\le a\] and if \[\left| x \right|\ge a\] then \[x\le -a\] or \[x\ge a\]. Here, ‘a’ must be a positive real number or it can be zero. If we have only the equality sign like \[\left| x \right|=a\] then we can directly remove the modulus sign and write the equation as \[x=\pm a\].