Question

How do you solve $3{\tan ^2}x = 1$ ?

Answer 1

Hint: Divide both the sides with $3$ to remove the constant part from the left hand side and isolate the trigonometric function. Then we take the square root of both the sides to find the value of $\tan x$. Then once we know the value of $\tan x$, we can divide both sides of the equation to find the value of angle $x$ and thus get our required answer.

Complete step-by-step solution:
The given expression is: $3{\tan ^2}x = 1$.
Now, we need to isolate our trigonometric function ${\tan ^2}x$ , in order to do so, we divide both the sides of the expression with $3$ so that our left hand side of the expression becomes free of any constant:
Therefore,
$ \Rightarrow {\tan ^2}x = \dfrac{1}{3}$
Now we take out the square –root on both the sides of the expression:
$\sqrt {{{\tan }^2}x} = \sqrt {\dfrac{1}{3}} $
$ \Rightarrow \tan x = \pm \dfrac{1}{{\sqrt 3 }}$ , thus we have two roots of $\tan x$ : $ + \dfrac{1}{{\sqrt 3 }}, - \dfrac{1}{{\sqrt 3 }}$ , because on taking out the square root of non-square numbers we get two values: positive and negative.
Taking the positive value of root:
$\tan x = \dfrac{1}{{\sqrt 3 }}$
Now, we know that $\tan \theta = \dfrac{1}{{\sqrt 3 }} = {30^ \circ }$
Here $x$ represents $\theta $ , therefore $\tan x = \dfrac{1}{{\sqrt 3 }} = {30^ \circ }$
Therefore $x = {30^ \circ }$ In the first quadrant. $x$ can also be $ + \dfrac{1}{{\sqrt 3 }}$ in the third quadrant as all functions of $\tan $ are positive here as shown in the picture below:

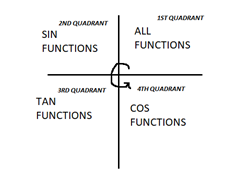
Therefore $\tan x = + \dfrac{1}{{\sqrt 3 }}$ when $x = {30^ \circ },\left( {{{180}^ \circ } + {{30}^ \circ }} \right) = {30^ \circ },{210^ \circ }$
Taking the negative value of root:
$\tan x = - \dfrac{1}{{\sqrt 3 }}$
Now, the value of $\tan x$ can be negative in the second and fourth quadrant.
Therefore the values of $x$ in the second quadrant can be $\left( {180 - {{30}^ \circ }} \right) = {150^ \circ }$ where ${180^ \circ }$ represent a complete transition from the First quadrant to the third quadrant.
In the fourth quadrant the value of $x = 360 - {30^ \circ }$, where ${360^ \circ }$ represents one complete circle around all the quadrants starting from the first quadrant.

Therefore the values of $x$ are: ${30^ \circ },{150^ \circ },{210^ \circ },{330^ \circ }$

Note: Some trigonometric values related to tan that needs to be remember are:
$\tan {30^ \circ } = \dfrac{1}{{\sqrt 3 }}$
$\tan {45^ \circ } = 1$
$\tan {60^ \circ } = \sqrt 3 $
$\tan {90^ \circ } = \infty $