Question

How do you solve \[2x-1=x+3\] ?

Answer 1

Hint: In these types of problems, what we can see is that there is a term x on both sides of the equation. Also, both the sides are linear i.e. having no \[2\] or higher powers of \[x\]. Thus, this problem can be easily solved by taking each side of the equation as two separate functions of \[x\] and draw graphs of these two functions. The point (or points) where these two graphs intersect is the solution of the equation.

Complete step by step answer:
In the given problem, taking the LHS and RHS to be two separate functions, we can write them as,
\[y=2x-1\].... Equation 1
\[y=x+3\] .... Equation 2
The general equation of a straight line is defined as \[y=mx+c\] , where \[m\] is defined as the slope of the line and \[c\] is defined as the y-intercept. Comparing equation 1 and equation 2 with the generalized definition of straight line, we see, in equation 1, \[2\] is the slope of the line, whereas \[-1\] is the y-intercept. Similarly, for equation 2, \[1\] is the slope of the line, whereas \[3\] is the y-intercept.
These functions being linear, their graphs will be mere straight lines. We now draw them on a graph paper using their intercept form. The x-intercept of equation 1 is \[\dfrac{1}{2}\] and that of equation 2 is \[-3\]. The y-intercept of equation 1 is \[-1\]and that of equation 2 is \[3\].

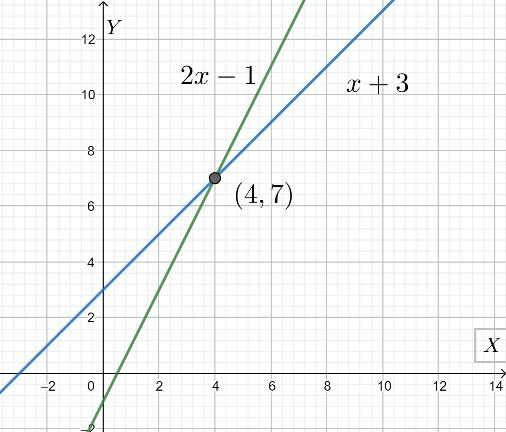
From the graph, it is clearly visible that the point of intersection of the two straight lines is \[\left( 4,7 \right)\]. This means that this point lies on both the lines, and is therefore a solution of the two equations, equation 1 and equation 2.

Therefore, we can conclude that \[x=4\] is a solution of the given equation.

Note: Drawing graphs is preferably the best method as it gives us a clear idea about the behaviour of each of the equations and at the same time, provides us the solutions of them. However, the problem could also be solved without graphs. We could take all the terms to one side of the equation and then directly find the value of \[x\].