
How do you graph \[y=x\ln x\]?
Answer
543k+ views
Hint: From the given question we have been asked to find the graph of the logarithmic function \[y=x\ln x\]. For this question we will find the first derivative to the function and also the second derivative and analyze the graph by finding the critical points. Later will find the intercept points of this graph. After doing this all process we will find the graph of the function.
Complete step by step answer:
Firstly, as we said before we will start by finding the first derivative of the function \[y=x\ln x\]. So, we get,
\[\Rightarrow y=x\ln x\]
Here we use the product rule of differentiation which is \[\Rightarrow \dfrac{d\left( uv \right)}{dx}=u\dfrac{dv}{dx}+v\dfrac{du}{dx}\]. So, we get,
\[\Rightarrow \dfrac{dy}{dx}=1\left( \ln x \right)+x\left( \dfrac{1}{x} \right)\]
\[\Rightarrow \dfrac{dy}{dx}=\left( \ln x \right)+1\]
Now, we can see that this will give us the graph of \[y=\ln x\] with a vertical transformation of one unit upwards.
Now, we will find the critical numbers, which will occur or we can find them when the derivative is equated to zero or is undefined.
The derivative will be undefined whenever \[x\le 0\], however the initial given function in question will be undefined in these cases too, so these critical numbers don’t count.
So, now when we equate the derivative to zero, we get,
\[\Rightarrow \ln x+1=0\]
\[\Rightarrow \ln x=-1\]
Now we will remove the logarithm. So, we get,
\[\Rightarrow \ln x=-1\]
\[\Rightarrow x=\dfrac{1}{e}\]
Now, we will check on both sides of this point.
Test point: \[\Rightarrow x=\dfrac{1}{6}\]
\[\Rightarrow \dfrac{dy}{dx}=\left( \ln x \right)+1\]
\[\Rightarrow \dfrac{dy}{dx}=\ln \left( \dfrac{1}{6} \right)+1\]
This is negative.
Test point: \[x=2\]
\[\Rightarrow \dfrac{dy}{dx}=\ln \left( 2 \right)+1\]
This is positive.
Therefore, \[\Rightarrow x=\dfrac{1}{e}\] is an absolute minimum. This also means there will be no absolute maximum.
Now, we will find the second derivative.
\[\Rightarrow \dfrac{dy}{dx}=\left( \ln x \right)+1\]
Here we use the formula \[\Rightarrow \dfrac{d\left( \ln x \right)}{dx}=\dfrac{1}{x}\].
\[\Rightarrow \dfrac{d}{dx}\left( \dfrac{dy}{dx} \right)=\dfrac{1}{x}\]
If we set this to zero to find the points of inflection, we find,
\[\Rightarrow \dfrac{1}{x}=0\]
\[\Rightarrow 1=0\]
This is a contradiction, so there are no points of inflection.
Finally, we analyze the intercepts.
There will be no y-intercept because \[\ln 0\] don’t have any real value.
\[\Rightarrow x\ln x=0\]
\[\Rightarrow x=0or1\]
But the initial function \[y=x\ln x\] is undefined at \[\Rightarrow x=0\]. Therefore, our one intercept is \[\left( 1,0 \right)\].
So, the graph will be as follows.
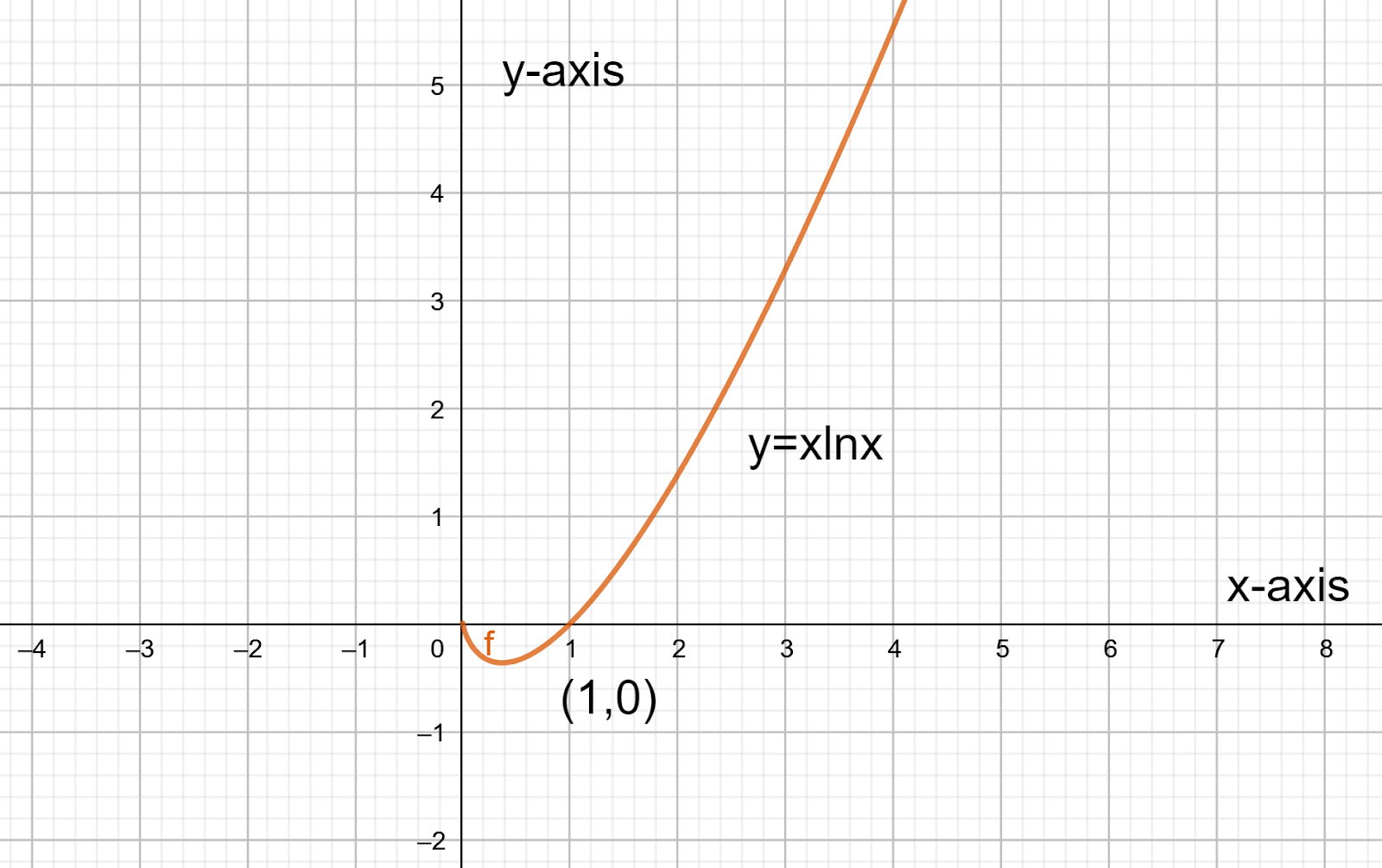
Note: Students must have good knowledge in the concept of differentiation and its applications. Students must not make any calculation mistakes. Students should know the basic differentiation formulae like,
The product rule or UV rule,
\[\Rightarrow \dfrac{d\left( uv \right)}{dx}=u\dfrac{dv}{dx}+v\dfrac{du}{dx}\]
And also the formula for logarithmic function which is as follows.
\[\Rightarrow \dfrac{d\left( \ln x \right)}{dx}=\dfrac{1}{x}\].
Complete step by step answer:
Firstly, as we said before we will start by finding the first derivative of the function \[y=x\ln x\]. So, we get,
\[\Rightarrow y=x\ln x\]
Here we use the product rule of differentiation which is \[\Rightarrow \dfrac{d\left( uv \right)}{dx}=u\dfrac{dv}{dx}+v\dfrac{du}{dx}\]. So, we get,
\[\Rightarrow \dfrac{dy}{dx}=1\left( \ln x \right)+x\left( \dfrac{1}{x} \right)\]
\[\Rightarrow \dfrac{dy}{dx}=\left( \ln x \right)+1\]
Now, we can see that this will give us the graph of \[y=\ln x\] with a vertical transformation of one unit upwards.
Now, we will find the critical numbers, which will occur or we can find them when the derivative is equated to zero or is undefined.
The derivative will be undefined whenever \[x\le 0\], however the initial given function in question will be undefined in these cases too, so these critical numbers don’t count.
So, now when we equate the derivative to zero, we get,
\[\Rightarrow \ln x+1=0\]
\[\Rightarrow \ln x=-1\]
Now we will remove the logarithm. So, we get,
\[\Rightarrow \ln x=-1\]
\[\Rightarrow x=\dfrac{1}{e}\]
Now, we will check on both sides of this point.
Test point: \[\Rightarrow x=\dfrac{1}{6}\]
\[\Rightarrow \dfrac{dy}{dx}=\left( \ln x \right)+1\]
\[\Rightarrow \dfrac{dy}{dx}=\ln \left( \dfrac{1}{6} \right)+1\]
This is negative.
Test point: \[x=2\]
\[\Rightarrow \dfrac{dy}{dx}=\ln \left( 2 \right)+1\]
This is positive.
Therefore, \[\Rightarrow x=\dfrac{1}{e}\] is an absolute minimum. This also means there will be no absolute maximum.
Now, we will find the second derivative.
\[\Rightarrow \dfrac{dy}{dx}=\left( \ln x \right)+1\]
Here we use the formula \[\Rightarrow \dfrac{d\left( \ln x \right)}{dx}=\dfrac{1}{x}\].
\[\Rightarrow \dfrac{d}{dx}\left( \dfrac{dy}{dx} \right)=\dfrac{1}{x}\]
If we set this to zero to find the points of inflection, we find,
\[\Rightarrow \dfrac{1}{x}=0\]
\[\Rightarrow 1=0\]
This is a contradiction, so there are no points of inflection.
Finally, we analyze the intercepts.
There will be no y-intercept because \[\ln 0\] don’t have any real value.
\[\Rightarrow x\ln x=0\]
\[\Rightarrow x=0or1\]
But the initial function \[y=x\ln x\] is undefined at \[\Rightarrow x=0\]. Therefore, our one intercept is \[\left( 1,0 \right)\].
So, the graph will be as follows.
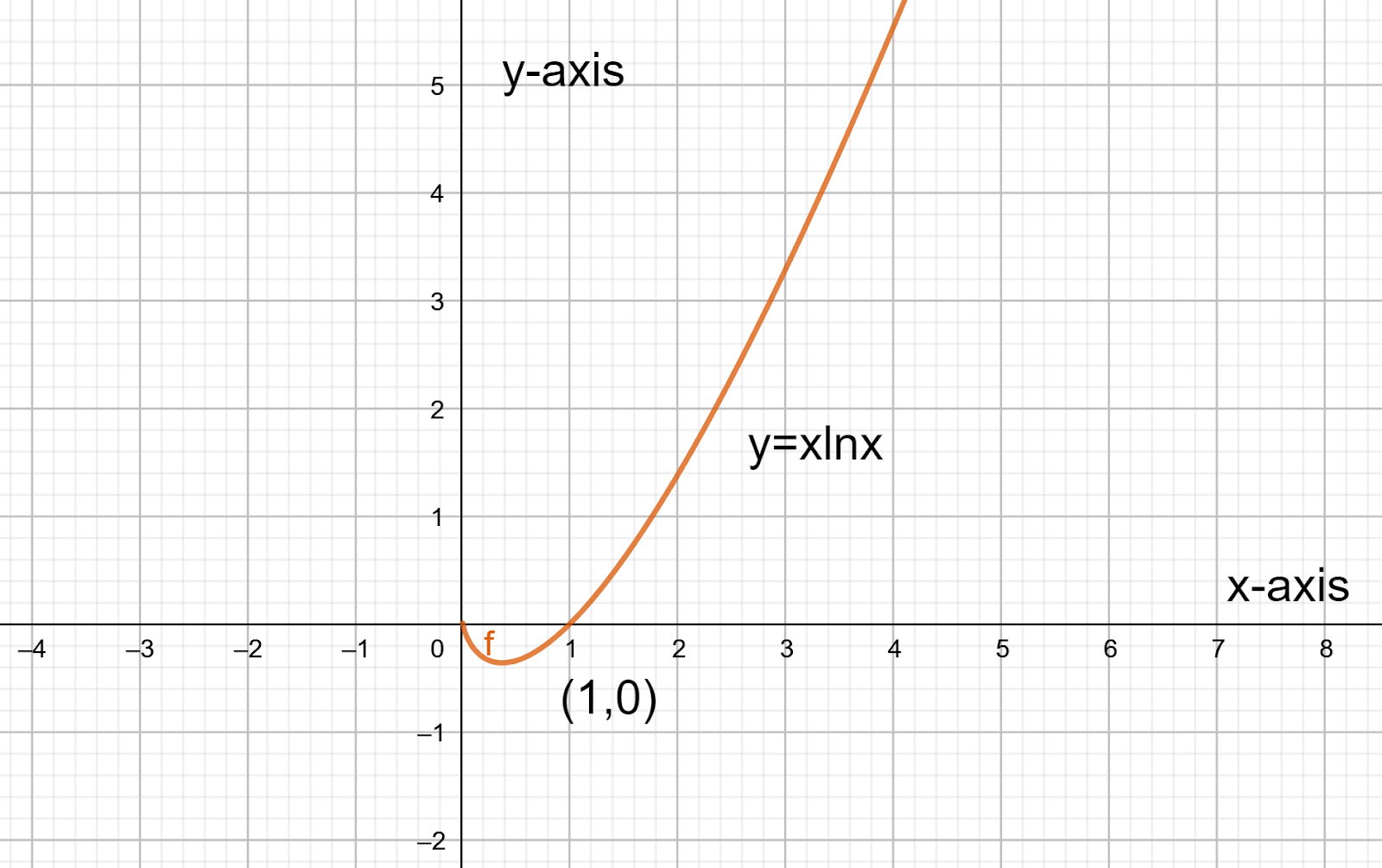
Note: Students must have good knowledge in the concept of differentiation and its applications. Students must not make any calculation mistakes. Students should know the basic differentiation formulae like,
The product rule or UV rule,
\[\Rightarrow \dfrac{d\left( uv \right)}{dx}=u\dfrac{dv}{dx}+v\dfrac{du}{dx}\]
And also the formula for logarithmic function which is as follows.
\[\Rightarrow \dfrac{d\left( \ln x \right)}{dx}=\dfrac{1}{x}\].
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Business Studies: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest Countries of the World?

What are the major means of transport Explain each class 12 social science CBSE

Draw a labelled sketch of the human eye class 12 physics CBSE

Why cannot DNA pass through cell membranes class 12 biology CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

Draw a neat and well labeled diagram of TS of ovary class 12 biology CBSE




