
How do you graph $y=\sin x$ and $y=\cos x$ .
Answer
533.1k+ views
Hint: To draw the graph of $y=\sin x$ , we have to consider different values of x and find the corresponding values of y. We have consider $x=0,\pm \dfrac{\pi }{2},\pm \pi ,\pm \dfrac{3\pi }{2},\pm 2\pi $ and find the corresponding values of y. To draw the graph of $y=\cos x$ , we will do the similar procedure.
Complete step by step solution:
We have to graph $y=\sin x$ and $y=\cos x$ . Let us first consider $y=\sin x$ . We have to consider different values of x and find the corresponding values of y.
Let us consider $x=0$ . We have to substitute the value of x in $y=\sin x$ .
$\Rightarrow y=\sin 0=0$
Let us consider $x=\dfrac{\pi }{2}$ .
\[\Rightarrow y=\sin \dfrac{\pi }{2}=1\]
We have to consider $x=\pi $ .
\[\Rightarrow y=\sin \pi =0\]
Let us consider $x=\dfrac{3\pi }{2}$ .
\[\Rightarrow y=\sin \dfrac{3\pi }{2}=-1\]
We have to consider $x=2\pi $ .
\[\Rightarrow y=\sin 2\pi =0\]
Now, let us consider the negative values. So when $x=-\dfrac{\pi }{2}$
\[\Rightarrow y=\sin \left( -\dfrac{\pi }{2} \right)\]
We know that $\sin \left( -\theta \right)=-\sin \theta $ .
\[\Rightarrow y=-\sin \left( \dfrac{\pi }{2} \right)=-1\]
We have to consider $x=-\pi $ .
\[\Rightarrow y=\sin \left( -\pi \right)=0\]
Let us consider $x=-\dfrac{3\pi }{2}$ .
\[\Rightarrow y=\sin \left( -\dfrac{3\pi }{2} \right)=-\sin \left( \dfrac{3\pi }{2} \right)=1\]
We have to consider $x=-2\pi $ .
\[\Rightarrow y=\sin \left( -2\pi \right)=0\]
Let us tabulate these values.
Now, let us plot the graph. Firstly, we have to plot the points in the graph. We have to convert $\pi $ into its numerical form, that is, 3.14 and plot the corresponding points. Then, we have to join the points as a curve. The graph of $y=\sin x$ is shown below.
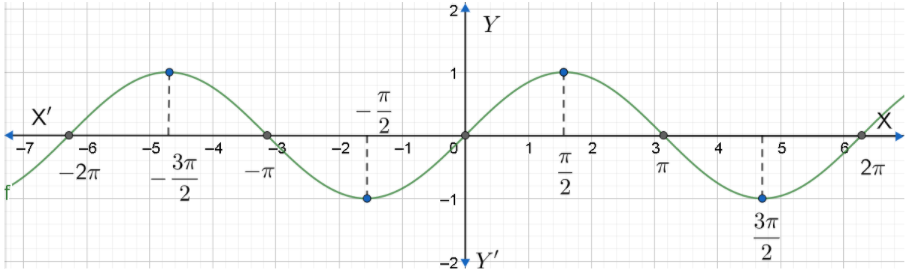
Now, let us consider $y=\cos x$ . Similar to the previous function, we will have to find the points to plot.
Let us consider $x=0$ . We have to substitute the value of x in $y=\cos x$ .
$\Rightarrow y=\cos 0=1$
Let us consider $x=\dfrac{\pi }{2}$ .
\[\Rightarrow y=\cos \dfrac{\pi }{2}=0\]
We have to consider $x=\pi $ .
\[\Rightarrow y=\cos \pi =-1\]
Let us consider $x=\dfrac{3\pi }{2}$ .
\[\Rightarrow y=\cos \dfrac{3\pi }{2}=0\]
We have to consider $x=2\pi $ .
\[\Rightarrow y=\cos 2\pi =1\]
Now, let us consider the negative values. So when $x=-\dfrac{\pi }{2}$
\[\Rightarrow y=\cos \left( -\dfrac{\pi }{2} \right)\]
We know that $\cos \left( -\theta \right)=\cos \theta $ .
\[\Rightarrow y=\cos \left( \dfrac{\pi }{2} \right)=0\]
We have to consider $x=-\pi $ .
\[\Rightarrow y=\cos \left( -\pi \right)=\cos \pi =-1\]
Let us consider $x=-\dfrac{3\pi }{2}$ .
\[\Rightarrow y=\cos \left( -\dfrac{3\pi }{2} \right)=\cos \left( \dfrac{3\pi }{2} \right)=0\]
We have to consider $x=-2\pi $ .
\[\Rightarrow y=\cos \left( -2\pi \right)=\cos \left( 2\pi \right)=1\]
Let us tabulate these values.
Now, let us plot the graph.
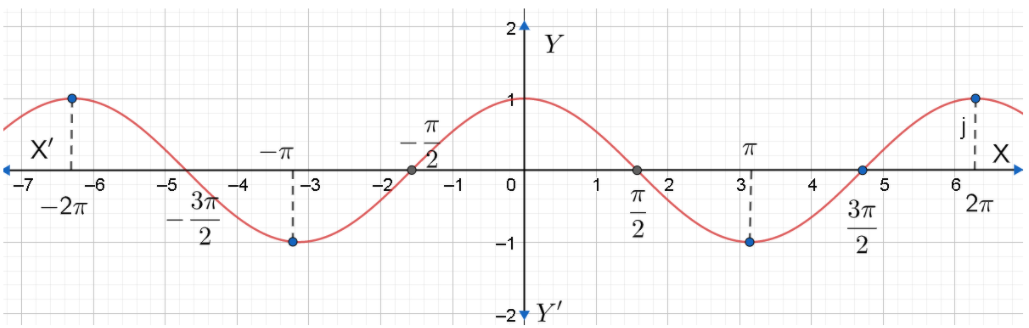
Note: We can also consider other angles also. Students have a chance of making mistakes by considering $\sin \left( -\theta \right)=\sin \theta $ and $\cos \left( -\theta \right)=-\cos \theta $ . We have considered the values of x to be $x=0,\pm \dfrac{\pi }{2},\pm \pi ,\pm \dfrac{3\pi }{2},\pm 2\pi $ as these values are easy to be plotted. We can find the domain and range of $y=\sin x$ and $y=\cos x$ . We know that the domain of a function is the complete set of possible values of the independent variable. Hence, the domain of sin x and cos x is $\left( -\infty ,\infty \right)$ . We know that range of a
Complete step by step solution:
We have to graph $y=\sin x$ and $y=\cos x$ . Let us first consider $y=\sin x$ . We have to consider different values of x and find the corresponding values of y.
Let us consider $x=0$ . We have to substitute the value of x in $y=\sin x$ .
$\Rightarrow y=\sin 0=0$
Let us consider $x=\dfrac{\pi }{2}$ .
\[\Rightarrow y=\sin \dfrac{\pi }{2}=1\]
We have to consider $x=\pi $ .
\[\Rightarrow y=\sin \pi =0\]
Let us consider $x=\dfrac{3\pi }{2}$ .
\[\Rightarrow y=\sin \dfrac{3\pi }{2}=-1\]
We have to consider $x=2\pi $ .
\[\Rightarrow y=\sin 2\pi =0\]
Now, let us consider the negative values. So when $x=-\dfrac{\pi }{2}$
\[\Rightarrow y=\sin \left( -\dfrac{\pi }{2} \right)\]
We know that $\sin \left( -\theta \right)=-\sin \theta $ .
\[\Rightarrow y=-\sin \left( \dfrac{\pi }{2} \right)=-1\]
We have to consider $x=-\pi $ .
\[\Rightarrow y=\sin \left( -\pi \right)=0\]
Let us consider $x=-\dfrac{3\pi }{2}$ .
\[\Rightarrow y=\sin \left( -\dfrac{3\pi }{2} \right)=-\sin \left( \dfrac{3\pi }{2} \right)=1\]
We have to consider $x=-2\pi $ .
\[\Rightarrow y=\sin \left( -2\pi \right)=0\]
Let us tabulate these values.
| x | $y=\sin x$ |
| 0 | 0 |
| $\dfrac{\pi }{2}$ | 1 |
| $\pi $ | 0 |
| $\dfrac{3\pi }{2}$ | -1 |
| $2\pi $ | 0 |
| $-\dfrac{\pi }{2}$ | -1 |
| $-\pi $ | 0 |
| $-\dfrac{3\pi }{2}$ | 1 |
| $-2\pi $ | 0 |
Now, let us plot the graph. Firstly, we have to plot the points in the graph. We have to convert $\pi $ into its numerical form, that is, 3.14 and plot the corresponding points. Then, we have to join the points as a curve. The graph of $y=\sin x$ is shown below.

Now, let us consider $y=\cos x$ . Similar to the previous function, we will have to find the points to plot.
Let us consider $x=0$ . We have to substitute the value of x in $y=\cos x$ .
$\Rightarrow y=\cos 0=1$
Let us consider $x=\dfrac{\pi }{2}$ .
\[\Rightarrow y=\cos \dfrac{\pi }{2}=0\]
We have to consider $x=\pi $ .
\[\Rightarrow y=\cos \pi =-1\]
Let us consider $x=\dfrac{3\pi }{2}$ .
\[\Rightarrow y=\cos \dfrac{3\pi }{2}=0\]
We have to consider $x=2\pi $ .
\[\Rightarrow y=\cos 2\pi =1\]
Now, let us consider the negative values. So when $x=-\dfrac{\pi }{2}$
\[\Rightarrow y=\cos \left( -\dfrac{\pi }{2} \right)\]
We know that $\cos \left( -\theta \right)=\cos \theta $ .
\[\Rightarrow y=\cos \left( \dfrac{\pi }{2} \right)=0\]
We have to consider $x=-\pi $ .
\[\Rightarrow y=\cos \left( -\pi \right)=\cos \pi =-1\]
Let us consider $x=-\dfrac{3\pi }{2}$ .
\[\Rightarrow y=\cos \left( -\dfrac{3\pi }{2} \right)=\cos \left( \dfrac{3\pi }{2} \right)=0\]
We have to consider $x=-2\pi $ .
\[\Rightarrow y=\cos \left( -2\pi \right)=\cos \left( 2\pi \right)=1\]
Let us tabulate these values.
| x | $y=\sin x$ |
| 0 | -1 |
| $\dfrac{\pi }{2}$ | 0 |
| $\pi $ | -1 |
| $\dfrac{3\pi }{2}$ | 0 |
| $2\pi $ | 1 |
| $-\dfrac{\pi }{2}$ | 0 |
| $-\pi $ | -1 |
| $-\dfrac{3\pi }{2}$ | 0 |
| $-2\pi $ | 1 |
Now, let us plot the graph.

Note: We can also consider other angles also. Students have a chance of making mistakes by considering $\sin \left( -\theta \right)=\sin \theta $ and $\cos \left( -\theta \right)=-\cos \theta $ . We have considered the values of x to be $x=0,\pm \dfrac{\pi }{2},\pm \pi ,\pm \dfrac{3\pi }{2},\pm 2\pi $ as these values are easy to be plotted. We can find the domain and range of $y=\sin x$ and $y=\cos x$ . We know that the domain of a function is the complete set of possible values of the independent variable. Hence, the domain of sin x and cos x is $\left( -\infty ,\infty \right)$ . We know that range of a
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Explain zero factorial class 11 maths CBSE

What organs are located on the left side of your body class 11 biology CBSE

Draw a labelled diagram of the human heart and label class 11 biology CBSE

What is 1s 2s 2p 3s 3p class 11 chemistry CBSE




