Question

How do you graph \[y + 4x = 1?\]

Answer 1

Hint: According to the question we have to determine the graph of the linear expression which is as given in the question is \[y + 4x = 1\]. So, First of all we have to substitute the different values of x and find the value of y for the different values of x. Same as we can substitute the values of y to obtain the values of x.
Now, we have to substitute the value $x = - 1$ in the linear expression \[y + 4x = 1\] which is as mentioned in the question.
Hence, on substituting the value $x = - 1$ in the expression we will obtain the two points to which we have to plot in the graph.
Now, we have to substitute the value of $x = 0$ in the linear expression \[y + 4x = 1\] which is as mentioned in the question.
Hence, on substituting the value $x = 0$ in the expression we will obtain the two points to which we have to plot in the graph.
Now, we have to substitute the value $x = 1$ in the linear expression \[y + 4x = 1\] which is as mentioned in the question.
Hence, on substituting the value $x = 1$ in the expression we will obtain the two points to which we have to plot in the graph.

Complete step-by-step solution:
Step 1: First of all we have to substitute the different values of x and find the value of y for the different values of x and same as we can substitute the values of y to obtain the values of x as mentioned in the solution hint.
Step 2: Now, we have to substitute the value $x = - 1$ in the linear expression \[y + 4x = 1\] which is as mentioned in the question. Hence,
$
   \Rightarrow y + 4( - 1) = 1 \\
   \Rightarrow y = 1 + 4 \\
   \Rightarrow y = 5
 $
Hence, on substituting the value $x = - 1$ in the expression we will obtain the two points to which we have to plot in the graph which are as below:
$ \Rightarrow A(x,y) = ( - 1,5)$
Step 3: Now, we have to substitute the value $x = 0$ in the linear expression \[y + 4x = 1\] which is as mentioned in the question. Hence,
$
   \Rightarrow y + 4(0) = 1 \\
   \Rightarrow y = 1
 $
Hence, on substituting the value $x = 0$ in the expression we will obtain the two points to which we have to plot in the graph which are as below:
$ \Rightarrow B(x,y) = (0,1)$
Step 4: Now, we have to substitute the value $x = 1$ in the linear expression \[y + 4x = 1\] which is as mentioned in the question. Hence,
$
   \Rightarrow y + 4(1) = 1 \\
   \Rightarrow y = 1 - 4 \\
   \Rightarrow y = - 3
 $
Hence, on substituting the value $x = 1$ in the expression we will obtain the two points to which we have to plot in the graph which are as below:
$ \Rightarrow C(x,y) = (1, - 3)$
Step 5: Now, we have to substitute the value $x = 1$ in the linear expression \[y + 4x = 1\] which is as mentioned in the question. Hence,
$
   \Rightarrow y + 4(1) = 1 \\
   \Rightarrow y = 1 - 4 \\
   \Rightarrow y = - 3
 $
Hence, on substituting the value $x = 1$ in the expression we will obtain the two points to which we have to plot in the graph which are as below:
$ \Rightarrow C(x,y) = (1, - 3)$
Step 6: Now, with the help of the points A, B and C which we have obtained in the previous steps we have to determine the line graph which is as below:

Hence, with the help of the points A, B and C we have determine the graph of the line \[y + 4x = 1\] which is as below:

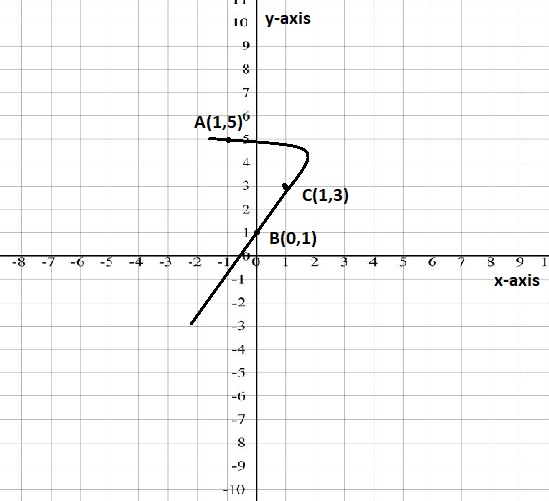
Note: To obtain the points it is necessary that we have to determine the values of y for the given expression which can be determined by placing the value of x as (-1,0,1) to obtain the value of y or vice-versa.
To obtain the graph it is necessary that we have to plot the points in the quadrant as $ \pm $ x-axis and $ \pm $ y-axis.