Question

How do you graph $ \theta = - {840^o} $

Answer 1

Hint: Convert between the given angle between $ {0^o} $ and $ {360^o} $ and then graph.
First, we are going to convert the given angles in such a way that it lies between $ {0^o} $ and $ {360^o} $ , then we will get some angle which lies in that interval, then we are going decide whether to go in clockwise direction or anti-clockwise direction to mark the mark and then we are going to mark and draw the angle which is required.

Complete step-by-step answer:
We are given an angle which has to be graphed whose measure is
 $ \theta = - {840^o} $
We have to first convert angle in such a way that it lies between $ {0^o} $ and $ {360^o} $ . It can be done by.
Further
The converted angle of $ - {840^o} $ which lies between $ {0^o} $ and $ {360^o} $ is .
Based on the nature of the sign of the obtained angle is negative it means we have to go clockwise from the $ {x^ + } $ semi axis or in other words we can say counterclockwise 240 degrees from the $ {x^ + } $ semi-axis.
Since we only have an angle, the radius can be any real value, so our equation describes a line. Just find the appropriate angle on the graph paper and trace a line through it.

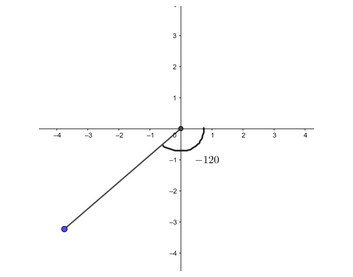
Note: We should always observe the nature of sign of angle whether it’s positive or negative as we have to decide on the base whether a positive axis of x or negative axis of x. This can only be done by knowing the nature of the sign of the given angle.