Question

How do you graph the line \[ - x = 7y - 7\] ?

Answer 1

Hint: In this question, we have to find out the graph from the given equation.
We need to evaluate two points to graph a line. For that we need to find out the x-intercept and y-intercept. For that we first need to put x and y equals to zero to find the x-intercept and y-intercept. Joining these two lines we can find out the required solution.

Complete step-by-step solution:
We need to find out the graph of the line \[ - x = 7y - 7\].
We only need two points to graph a line. With this idea we take advantage of the two convenient points which can easily be solved algebraically from the equation of the line, namely the x intercept
\[\left( {x,0} \right)\] and y-intercept \[\left( {0,y} \right)\] .
To find the x-intercept, let \[y = 0\] then solve for x.
Hence putting \[y = 0\], we get from the given line,
\[ \Rightarrow - x = 7 \times 0 - 7\]
Solving we get,\[ - x = 0 - 7\]
Or, \[x = 7\]
To find the y-intercept, let \[x = 0\] then solve for y.
Hence putting\[x = 0\], we get from the given line,
\[ \Rightarrow - 0 = 7 \times y - 7\]
Solving we get, \[7y = 7\]
Or,\[y = 1\]
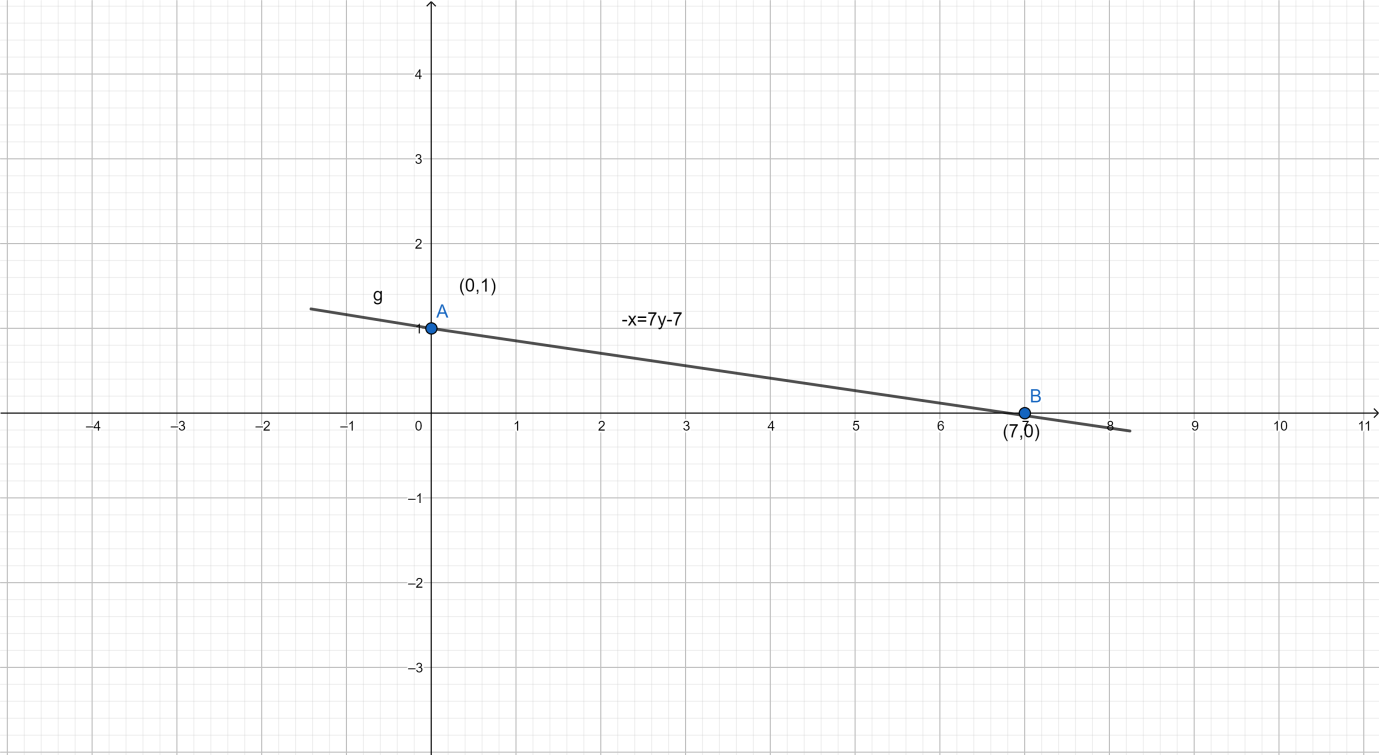
Thus the two points we get \[\left( {7,0} \right),\left( {0,1} \right)\].
Now we need to connect the two points using a ruler.

Note: A line is simply an object in geometry that is characterized under zero width objects that extends on both sides. A straight line is just a line with no curves. So, a line that extends to both sides till infinity and has no curves is called a straight line.
In geometry, the notion of line or straight line was introduced by ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects, which are often described in terms of two points or referred to using a single letter.