Question

How do you graph $ r = 2\sin \theta $ ?

Answer 1

Hint: The given equation is in the polar form of a conic section. To graph this equation on a cartesian plane we have to convert this equation into standard form or rectangular form. To convert this equation we can use the following conversions,
 $
  x = r\cos \theta \\
  y = r\sin \theta \;
  $
where $ \theta $ is the angle that the line joining origin and the general point makes with the x-axis and $ r $ is the magnitude or the distance of the point from origin given as $ {r^2} = {x^2} + {y^2} $ .

Complete step by step solution:
We have been given to graph the equation $ r = 2\sin \theta $ .
Since this equation includes the angle $ \theta $ and the magnitude $ r $ , this is in the polar form. To graph this equation we will first convert it into standard form or rectangular form such that we get an equation in terms of $ x $ and $ y $ . We can use $ x = r\cos \theta ,\;\;y = r\sin \theta \;\;and\;\;{r^2} = {x^2} + {y^2} $ .
From $ y = r\sin \theta $ , we have $ \sin \theta = \dfrac{y}{r} $ .
From $ {r^2} = {x^2} + {y^2} $ , we have $ r = \sqrt {{x^2} + {y^2}} $
Thus the given equation becomes,
 $
  r = 2\sin \theta \\
   \Rightarrow \sqrt {{x^2} + {y^2}} = 2\dfrac{y}{r} = \dfrac{{2y}}{{\sqrt {{x^2} + {y^2}} }} \\
   \Rightarrow {x^2} + {y^2} = 2y \;
  $
We have the coefficient of \[{x^2}\] is equal to the coefficient of \[{y^2}\]. So this equation will represent a circle in the cartesian plane.
We can simplify the equation as,
 $
  {x^2} + {y^2} = 2y \\
   \Rightarrow {x^2} + {y^2} - 2y = 0 \\
   \Rightarrow {x^2} + {y^2} - 2y + 1 = 1 \\
   \Rightarrow {x^2} + {\left( {y - 1} \right)^2} = {1^2} \;
  $
Thus the circle is centered at the point $ \left( {0,1} \right) $ and the radius is $ 1 $ .
This can be drawn on the graph as follows,

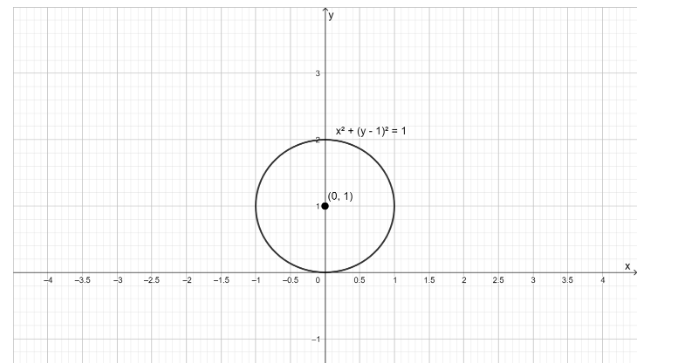
Hence, this is the graph of the given equation. Here $ r $ is the distance of the general point on the curve from origin and $ \theta $ is the angle that the line joining the origin and the general point will make with the x-axis.

Note: We converted the given polar form of the equation into the rectangular form to graph the equation in a cartesian plane. The rectangular form is given in terms of $ x $ and $ y $ . After the conversion we have to determine what type of curve this equation represents or else we have to find the critical points using the derivatives.