Question

The period of a conical pendulum in terms of its length $\left( l \right)$, semi vertical angle $\left( \theta \right)$ and acceleration due to gravity $\left( g \right)$ is __________
$\begin{align}
  & \text{A}\text{. }\dfrac{1}{2\pi }\sqrt{\dfrac{l\cos \theta }{g}} \\
 & \text{B}\text{. }\dfrac{1}{2\pi }\sqrt{\dfrac{l\sin \theta }{g}} \\
 & \text{C}\text{. 4}\pi \sqrt{\dfrac{l\cos \theta }{4g}} \\
 & \text{D}\text{. 4}\pi \sqrt{\dfrac{l\tan \theta }{g}} \\
\end{align}$

Answer 1

Hint: A conical pendulum has a mass attached to a string along the vertical. The mass executes circular motion in the horizontal plane. For calculating the time period of a conical pendulum, we need to use the expression of Newton's second law of motion. The tension along the string can be resolved in the x-axis and the y-axis. Along vertical, there should be no acceleration of the mass.

Complete answer:
A conical pendulum is a system of a mass attached to a nearly massless string that is held at the opposite end and swung in the horizontal circles. It doesn't take much effort to keep the mass moving at a constant angular velocity in a circle of constant radius.

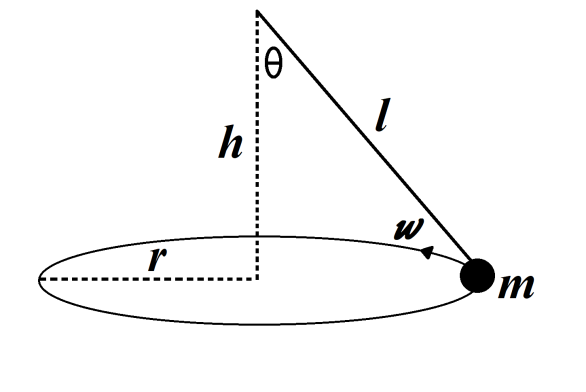
$h$ is the distance from the plane of the circular motion to where the string is attached
$r$ is the radius of the circular path in meters
$\theta $ is the angle between h and the string in degrees
$l$ is the length of the string in meters
$m$ is the mass of mass at the end of the string in kilograms
$\omega $ is the angular velocity of the mass in radians-per-second
Using Newton’s second law of motion,
$F=ma$
Where,
$F$ is the force acting on a body
$m$ is the mass of the body
$a$ is the acceleration of the body

Force-body diagram of the mass of the pendulum:

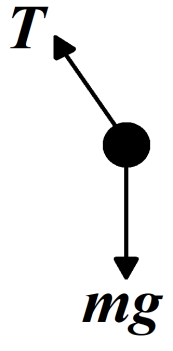
Resolving tension vector along x-axis and y-axis:

Let's plug in the vertical forces acting on the mass into $\sum{F=ma}$ , where the acceleration of the mass will be zero because the mass is not accelerating vertically.
Finding the tension in the string,
$T\cos \theta =mg$
And,
$T\sin \theta =\dfrac{m{{v}^{2}}}{r}$
Eliminating $T$, we get,
$\operatorname{Tan}\theta =\dfrac{{{v}^{2}}}{rg}$
We get,
$v=\sqrt{rg\tan \theta }$
We have,
$\tan \theta =\dfrac{r}{h}$
Therefore,
$\begin{align}
  & v=\sqrt{rg\times \dfrac{r}{h}} \\
 & v=\sqrt{{{r}^{2}}g\times \dfrac{l}{hl}} \\
\end{align}$
We have,
$\cos \theta =\dfrac{h}{l}$
Therefore,
$v=\sqrt{\dfrac{{{r}^{2}}g}{l\cos \theta }}$
Or,
$\dfrac{v}{r}=\sqrt{\dfrac{g}{l\cos \theta }}$
Time period of conical pendulum is given as,
$\begin{align}
  & T=\dfrac{2\pi r}{v} \\
 & T=2\pi \sqrt{\dfrac{l\cos \theta }{g}} \\
\end{align}$
Or,
$T=4\pi \sqrt{\dfrac{l\cos \theta }{4g}}$
The period of a conical pendulum is given as $T=4\pi \sqrt{\dfrac{l\cos \theta }{4g}}$

So, the correct answer is “Option C”.

Note:
A simple pendulum is a special case of a conical pendulum in which the angle made by the string with the vertical is zero. Time period of a pendulum can be calculated by applying Newton's second law of motion, which gives us the time period of a pendulum in terms of length of string, semi vertical angle and the radius of the circular path.