
How do you graph \[\ln x\]?
Answer
566.7k+ views
Hint: The logarithm base b of a number n is the number x that when b is raised to \[{{x}^{th}}\] power, the resulting value is n. That is, this can be written as \[{{\log }_{b}}n=x\Rightarrow {{b}^{x}}=n\]. The logarithm with base \[e\] is called the natural logarithm representing the \[\ln \] function. So, we can write the logarithm base \[e\] of a number n is the number x which can be expressed in exponents as \[\ln n={{\log }_{e}}n=x\Rightarrow {{e}^{x}}=n\].
Complete step by step answer:
\[\ln \] is called the natural logarithm with base \[e\] and \[\ln x\]is also called an inverse of exponential function\[{{e}^{x}}\]. \[e\] is an irrational number which is a constant and its value is 2.718281828459. It can also be written as \[{{\log }_{e}}x\]. \[\ln x\]is undefined when \[x\underline{<}0\].
If we observe the given expression, we get to know that the base of this logarithmic function is \[e\] which is a natural logarithm.
We can directly find the logarithmic graph by taking the image of a graph of an exponential function with respect to any of the lines\[y=\pm x\] based on the existence of the graphs.
The below graph says that \[\ln x\] is the image of \[{{e}^{x}}\] through \[y=x\].
In the below graph, first we draw a graph of \[{{e}^{x}}\]and \[y=x\] then we take the image of \[{{e}^{x}}\] which is the graph of \[\ln x\]. In this way we draw the graph of \[\ln x\].
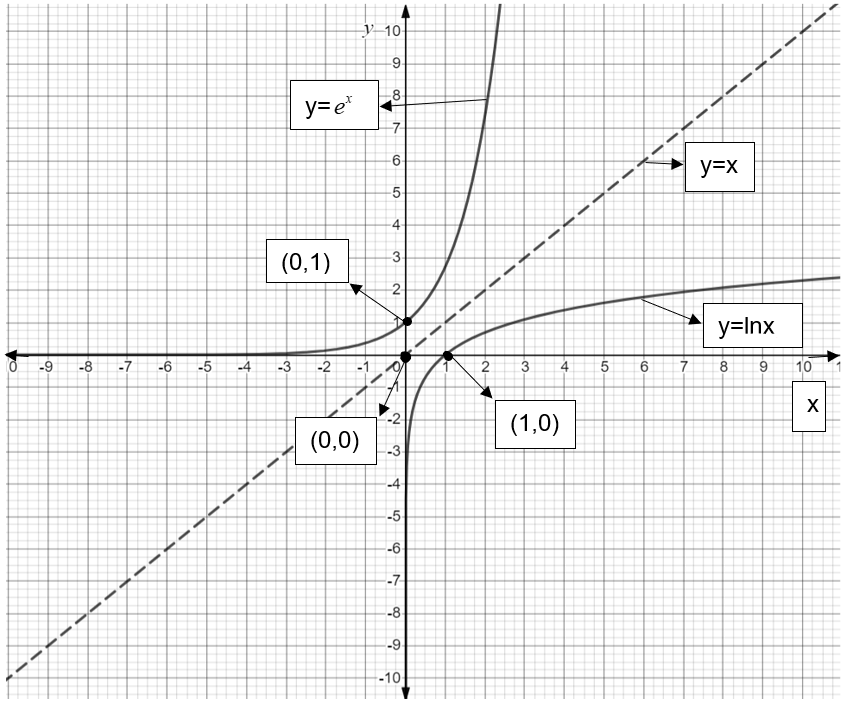
The graph of \[y=\ln x\] is shown in the below figure:
Note:
We should be thorough with the logarithm and exponent concept to avoid mistakes like taking base 10 for \[\ln \] function instead of \[e\]. \[\ln x\] is valid only for values \[x>0\]. \[\ln x\] meets \[x-axis\]only at \[(1,0)\]. \[{{e}^{x}}\]gives only positive values.
Complete step by step answer:
\[\ln \] is called the natural logarithm with base \[e\] and \[\ln x\]is also called an inverse of exponential function\[{{e}^{x}}\]. \[e\] is an irrational number which is a constant and its value is 2.718281828459. It can also be written as \[{{\log }_{e}}x\]. \[\ln x\]is undefined when \[x\underline{<}0\].
If we observe the given expression, we get to know that the base of this logarithmic function is \[e\] which is a natural logarithm.
We can directly find the logarithmic graph by taking the image of a graph of an exponential function with respect to any of the lines\[y=\pm x\] based on the existence of the graphs.
The below graph says that \[\ln x\] is the image of \[{{e}^{x}}\] through \[y=x\].
In the below graph, first we draw a graph of \[{{e}^{x}}\]and \[y=x\] then we take the image of \[{{e}^{x}}\] which is the graph of \[\ln x\]. In this way we draw the graph of \[\ln x\].

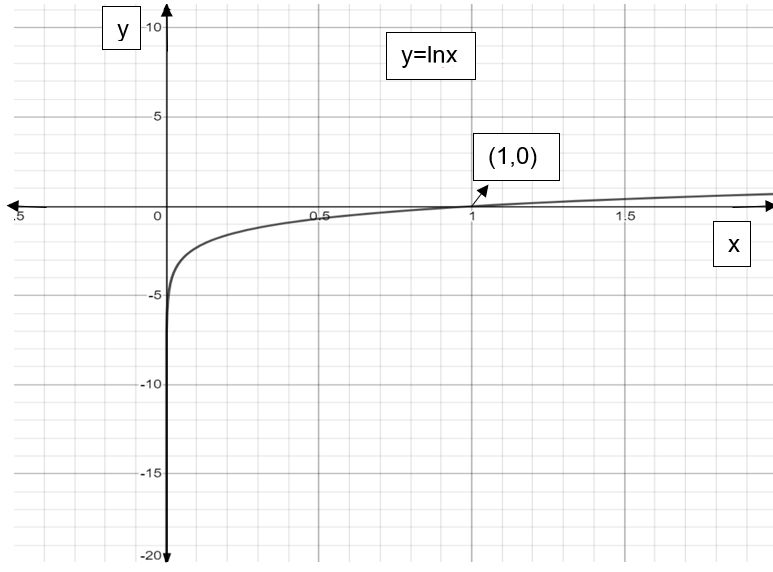
The graph of \[y=\ln x\] is shown in the below figure:

Note:
We should be thorough with the logarithm and exponent concept to avoid mistakes like taking base 10 for \[\ln \] function instead of \[e\]. \[\ln x\] is valid only for values \[x>0\]. \[\ln x\] meets \[x-axis\]only at \[(1,0)\]. \[{{e}^{x}}\]gives only positive values.
Recently Updated Pages
Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Class 10 Question and Answer - Your Ultimate Solutions Guide

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Trending doubts
State and prove converse of BPT Basic Proportionality class 10 maths CBSE

State BPT theorem and prove it class 10 maths CBSE

A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Find the area of the minor segment of a circle of radius class 10 maths CBSE

Write a letter to the editor of a newspaper explaining class 10 english CBSE

What is a "free hit" awarded for in limited-overs cricket?




