Question

How do you graph $f\left( x \right)=2+\ln x$?

Answer 1

Hint: In this question we will first understand how the graph of $f(x)={{e}^{x}}$ works and the asymptote of the graph and then we will understand how to graph of $f(x)=\ln x$ works and then we will deduce what happens when a constant value is added to the function and then plot the graph for the same.

Complete step-by-step solution:
We have the given logarithmic function as $f\left( x \right)=2+\ln x$ .
To understand how the graph of this function flows, we will first look at the graph of the exponential function which is denoted as $f(x)={{e}^{x}}$.

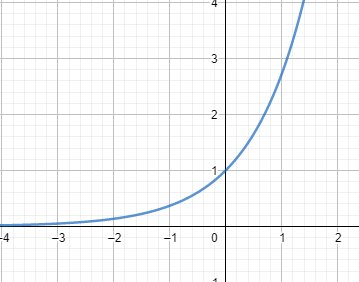
It can be seen from the graph that has a horizontal asymptote which is at $y=0$ and it passes through the point $(0,1)$ on the graph.
Now consider the graph of the logarithmic function, it is the inverse of the graph of the exponential function and it is denoted as $f(x)=\ln x$

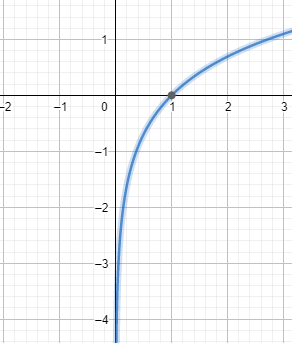
From the graph we can see that the function has a vertical asymptote which is it $x=0$ and it passes through the point $(1,0)$ on the graph.
Therefore, from the above graph we can deduce that the graph of $f\left( x \right)=2+\ln x$ will be vertically shifted or vertically transformed of the line $\ln x$ which is shifted by $2$. It will have the asymptote at $x=0$ and will pass through the point which is $2$ units shifted in the $y$ axis, which can be written as $(1,0+2)$ which can be simplified as $(1,2)$.
On plotting the graph, we get:

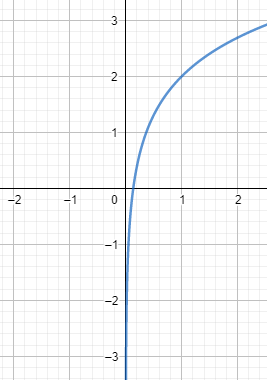
Which is the required solution.

Note: An asymptote is a line on the graph through which the graph passes to and reaches either positive or negative infinity.
Logarithm is used to simplify a mathematical expression, it converts multiplication to addition, division to subtraction and exponents to multiplication.
The most commonly used bases in logarithm are $10$ and $e$ which has a value of approximate $2.713....$