Question

Here the steps of construction of an equilateral triangle one whose altitudes measure 5 cm are given. In these steps, one step is wrong. Which step does not fit in the steps of construction?
STEPS OF CONSTRUCTION: \[\]
(i) Draw a line $XY$\[\]
(ii) Mark any point P on it
(iii) From P, draw $PQ\bot XY$ \[\]
 (iv) From P, set off $PA=5$ cm cutting $PQ$ at $A$\[\]
 (v) Construct $\angle PAB={{60}^{\circ }}$and $\angle PAC={{60}^{\circ }}$, meeting $XY$ at B and C respectively, making $\Delta ABC$.\[\]
A. (i) only \[\]
B.(ii) only\[\]
C. (iii) only\[\]
D. (iv) only \[\]

Answer 1

Hint: We follow the construction as asked in the question step by step and check whether each step is correct or not. We use the fact that all the angles of an equilateral triangle have the measure ${{60}^{\circ }}$and then check whether $\angle BAC={{60}^{\circ }}$ or not. \[\]

Complete step-by-step solution
We are given in the question the steps of construction of an equilateral triangle one whose altitude measures 5 cm. We follow the steps one by one. \[\]
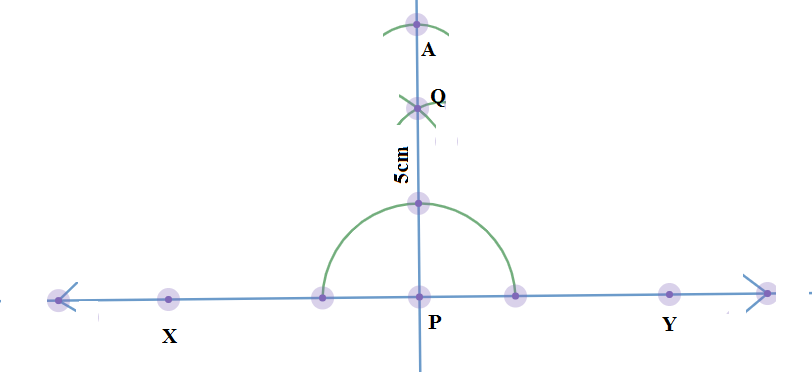
(i) We draw a line $XY$ with a rule on which one side of the equilateral triangle will lie. \[\]

(ii) We mark a point P on it which will serve as the foot of the perpendicular or altitude. This step is correct.

(iii)We draw the perpendicular line PQ of XY passing through the point P by bisecting the arc of ${{180}^{\circ }}$ with rounder at the point P. We denote Q as the point of intersection of bisecting arcs. This step is correct. \[\]
 

(iv) We take an arc of 5cm using the scale and the rounder and intersect PQ at a certain point. We denote the point as A. Now AP is our altitude of triangle ABC. This step is correct. \[\]

(v) We draw construct $\angle PAB={{60}^{\circ }}$and $\angle PAC={{60}^{\circ }}$ by drawing rays using the rounder and taking the arc of equal width on the point A on both side which meets $XY$ at B and C respectively.\[\]
 

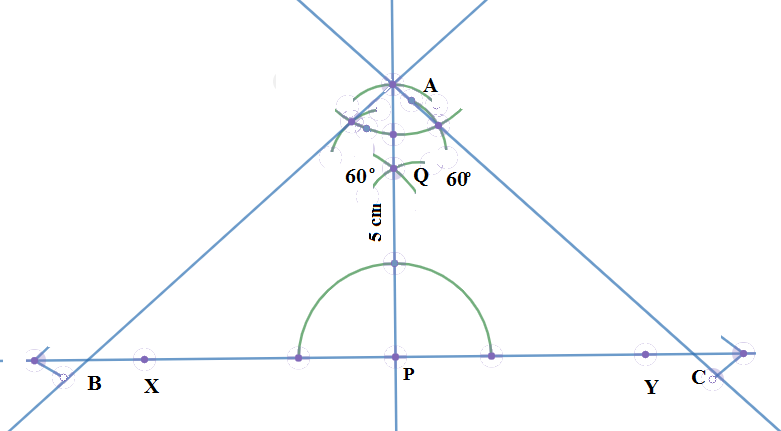
We join AB and AC to get the triangle ABC. We know that the triangle ABC will be equilateral when all the angles are equal and of measure ${{60}^{\circ }}$ which means $\angle ABC=\angle ACB=\angle BAC={{60}^{\circ }}$, but we see that according to our construction
\[\angle BAC=\angle PAB+\angle PAC={{60}^{\circ }}+{{60}^{\circ }}={{120}^{\circ }}\]
So this step is incorrect. We are asked to find the step that does not fit in the steps of construction which we now obtained as step (v) only. So the correct choice is D.\[\]

Note: The obtained triangle is not equilateral but isosceles whose two angles are equal, $\angle ABC=\angle ACB={{30}^{\circ }}$. We also note that equilateral triangles must have equal sides too. If we want to make the triangle ABC equilateral we have to change the construction of construct $\angle PAB={{60}^{\circ }}$ and $\angle PAC={{60}^{\circ }}$to $\angle PAB={{30}^{\circ }}$and $\angle PAC={{30}^{\circ }}$.