Question

What is the height of a square pyramid of base edge 12 cm and slant height 10 cm? Also find its volume.

Answer 1

Hint: For solving the given problem, we should know about the basics of the square pyramid. The height of a square pyramid is given by $\sqrt{{{s}^{2}}-{{\left( \dfrac{a}{2} \right)}^{2}}}$. Here s is the slant height of the square pyramid and a is the length of the square base edge. The volume of the square pyramid is given by ${{a}^{2}}\left( \dfrac{h}{3} \right)$ . Here, a is the length of the square base edge and h is the height of the pyramid.

Complete step-by-step answer:
Before solving the question, we try to understand the basics of geometry of a square pyramid. We have the below figure of a square pyramid. The quantities of interest to us are the square base edge (a), slant height (s) and the height of the square pyramid (h). These parameters can be seen on the figure below.

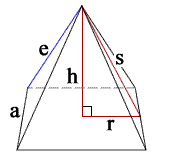
Now, in the given question, we have, square pyramid of base edge 12 cm and slant height 10 cm. That is, we have a = 12 cm and s = 10 cm. Now, we have the formula for height given by –
h = $\sqrt{{{s}^{2}}-{{\left( \dfrac{a}{2} \right)}^{2}}}$
Substituting the values of s and a, we have,
h = $\sqrt{{{10}^{2}}-{{\left( \dfrac{12}{2} \right)}^{2}}}$
h = $\sqrt{{{10}^{2}}-{{6}^{2}}}$
h = $\sqrt{64}$ = 8 cm
Now, to find the volume of the square pyramid, the formula is given as-
Volume = ${{a}^{2}}\left( \dfrac{h}{3} \right)$
Volume = ${{12}^{2}}\left( \dfrac{8}{3} \right)$
Volume = 384 $c{{m}^{3}}$
Thus, the height of the square pyramid in the problem is 8 cm and the volume is 384 $c{{m}^{3}}$ .

Note: While solving the questions related to three dimensional geometries, we should first start by visualising the figure in terms of the known quantities and then proceed to solve the question. Although height of the square pyramid can be simply calculated by the use of Pythagoras theorem, it is suggested to memorize the formula for the volume of the square pyramid since its calculation is not trivial.