Question

What happens to an electric dipole placed in a uniform electric field .Drive necessary expression.

Answer 1

Hint: In order to answer this question, first we will find the uniform electric field equation and then dipole moment in an uniform electric field we observe the situation. Now, consider a dipole with charges $ + q$ and $ - q$ forming a dipole since they are a distance d away from each other. Let it be placed in a uniform electric field of strength E such that the axis of the dipole forms an angle $\theta $ with the electric field. $F = m \times a$

Formula used:
$
  \overline E = E \circ \hat i \\
  \tau = \bar r \times \bar F \\
  F = qE \\
 $

Complete step by step solution:

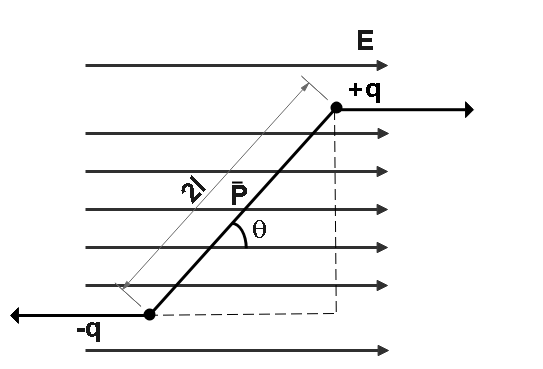
As we know that In an uniform electric field, the field lines are parallel to each other and is given by
$\overline E = E \circ \hat i$
Where $\overline E $ is an electric vector field with $E \circ $ as magnitude.
And dipole moment $\overline P = q(2l)\hat i$.
Here $\overline P $ is the dipole moment and $\hat i$ represents the direction.
And the distance between the two charges is $2l$.
Here we keep a dipole in a uniform electric field $\overline E $ which makes an angle $\theta $ with electric field lines.
Here force acts on both $ + q$ and $ - q$ charges.
So,
$F = \pm qE\hat i$
Here force is able to rotate the dipole which causes torque to generate which is:-
$
  rsin\theta = 2l\sin \theta \\
  {\text{and}} \\
  F = qE \\
 $

Additional Information:
In mechanics, a pair of equal parallel forces that are opposite in direction. The only effect of a couple is to produce or prevent the turning of a body. The turning effect, or moment, of a couple is measured by the product of the magnitude of either force and the perpendicular distance between the action lines of the forces.

Note:
In an uniform electric field, the net force on a dipole will always be zero but torque is zero for $\theta = {0^ \circ }$ and maximum when $\theta = {90^ \circ }$. We should use the formula and concept correctly without any confusion and also remember the important points.