
How do you graph\[f\left( x \right)=\left| x-6 \right|\] ?
Answer
556.8k+ views
Hint: For the given problem we have to plot the graph for the equation \[f\left( x \right)=\left| x-6 \right|\].For that we have to find the absolute vertex for the graph. Then we have to find some more points to plot the graph. With all these points we can draw our graph.
Complete step by step answer:
For the given problem we are given to plot a graph for the equation\[f\left( x \right)=\left| x-6 \right|\].
Let us consider the given equation as equation (1).
\[f\left( x \right)=\left| x-6 \right|........\left( 1 \right)\]
Let us find the vertex for the given equation. To find the x-coordinate of the vertex set the value \[x-6\]is equal to 0.
\[\begin{align}
& \Rightarrow x-6=0 \\
& \Rightarrow x=6 \\
\end{align}\]
Let us replace x value with 6 in equation (1), we get
\[\begin{align}
& \Rightarrow y=|x-6| \\
& \Rightarrow y=|6-6| \\
& \Rightarrow y=0 \\
\end{align}\]
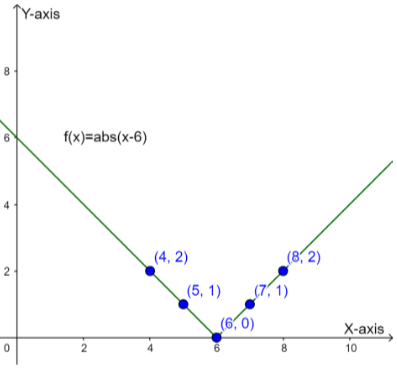
Therefore the absolute vertex for the equation is (6, 0).
Let us consider,
Vertex = (6, 0).
For each value of ‘x’, there is only one ‘y’ value. Let us select ‘x’ values from the domain. It would be useful to select the values so that they are around the x value of the absolute value vertex.
Substitute the ‘x’ value 4 into\[f\left( x \right)=|x-6|\]. In this case, the point is (4, 2).
Replace the variable x with 4 in the expression.
\[\begin{align}
& \Rightarrow f\left( 4 \right)=|\left( 4 \right)-6| \\
& \Rightarrow 2 \\
\end{align}\]
Therefore, the ordered pair will be (4, 2).
Repeating the same steps for\[x=5\], then the ordered pair will be (5, 1).
The absolute value can be graphed using the points around the vertex.
(6, 0); (4, 2) (5, 1); (7, 1); (8, 2).
Therefore graph of the equation will be-
Note:
Modulus of x means the absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. We should note that a point given equation is a modulus equation, so we will not find any negative values of x and y in the graph. Every modulus graph will be a ‘V’ shaped graph.
Complete step by step answer:
For the given problem we are given to plot a graph for the equation\[f\left( x \right)=\left| x-6 \right|\].
Let us consider the given equation as equation (1).
\[f\left( x \right)=\left| x-6 \right|........\left( 1 \right)\]
Let us find the vertex for the given equation. To find the x-coordinate of the vertex set the value \[x-6\]is equal to 0.
\[\begin{align}
& \Rightarrow x-6=0 \\
& \Rightarrow x=6 \\
\end{align}\]
Let us replace x value with 6 in equation (1), we get
\[\begin{align}
& \Rightarrow y=|x-6| \\
& \Rightarrow y=|6-6| \\
& \Rightarrow y=0 \\
\end{align}\]
Therefore the absolute vertex for the equation is (6, 0).
Let us consider,
Vertex = (6, 0).
For each value of ‘x’, there is only one ‘y’ value. Let us select ‘x’ values from the domain. It would be useful to select the values so that they are around the x value of the absolute value vertex.
Substitute the ‘x’ value 4 into\[f\left( x \right)=|x-6|\]. In this case, the point is (4, 2).
Replace the variable x with 4 in the expression.
\[\begin{align}
& \Rightarrow f\left( 4 \right)=|\left( 4 \right)-6| \\
& \Rightarrow 2 \\
\end{align}\]
Therefore, the ordered pair will be (4, 2).
Repeating the same steps for\[x=5\], then the ordered pair will be (5, 1).
The absolute value can be graphed using the points around the vertex.
(6, 0); (4, 2) (5, 1); (7, 1); (8, 2).
| X | Y |
| 4 | 2 |
| 5 | 1 |
| 6 | 0 |
| 7 | 1 |
| 8 | 2 |
Therefore graph of the equation will be-

Note:
Modulus of x means the absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. We should note that a point given equation is a modulus equation, so we will not find any negative values of x and y in the graph. Every modulus graph will be a ‘V’ shaped graph.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Explain zero factorial class 11 maths CBSE

What organs are located on the left side of your body class 11 biology CBSE

Draw a labelled diagram of the human heart and label class 11 biology CBSE

What is 1s 2s 2p 3s 3p class 11 chemistry CBSE




