Question

How do you graph $ y = \sqrt {x + 1} $ , compare it to the parent graph and what is the domain and range?

Answer 1

Hint: In this problem we have given an equation and we are asked to draw the graph for the given equation and also we asked to compare the graph of the given equation to the parent graph. Also we have to find the domain and range of the graph of the given equation. Here the parent graph may also look like the given equation’s graph but we can see some changes.

Complete Step by Step Solution:
Given that $ y = \sqrt {x + 1} $
Now we have to draw the graph for the given equation.

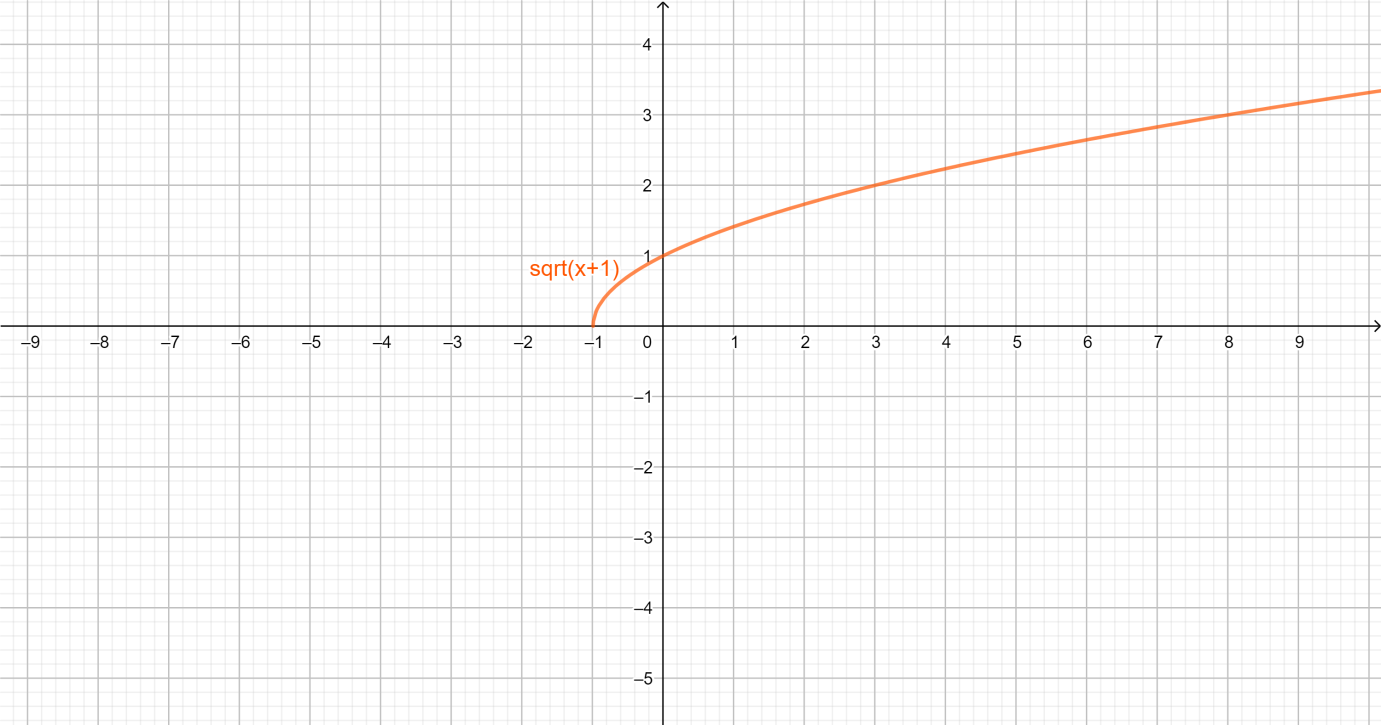
We have asked to compare the graph of the given equation to the parent graph. So now we need to draw the parent graph.

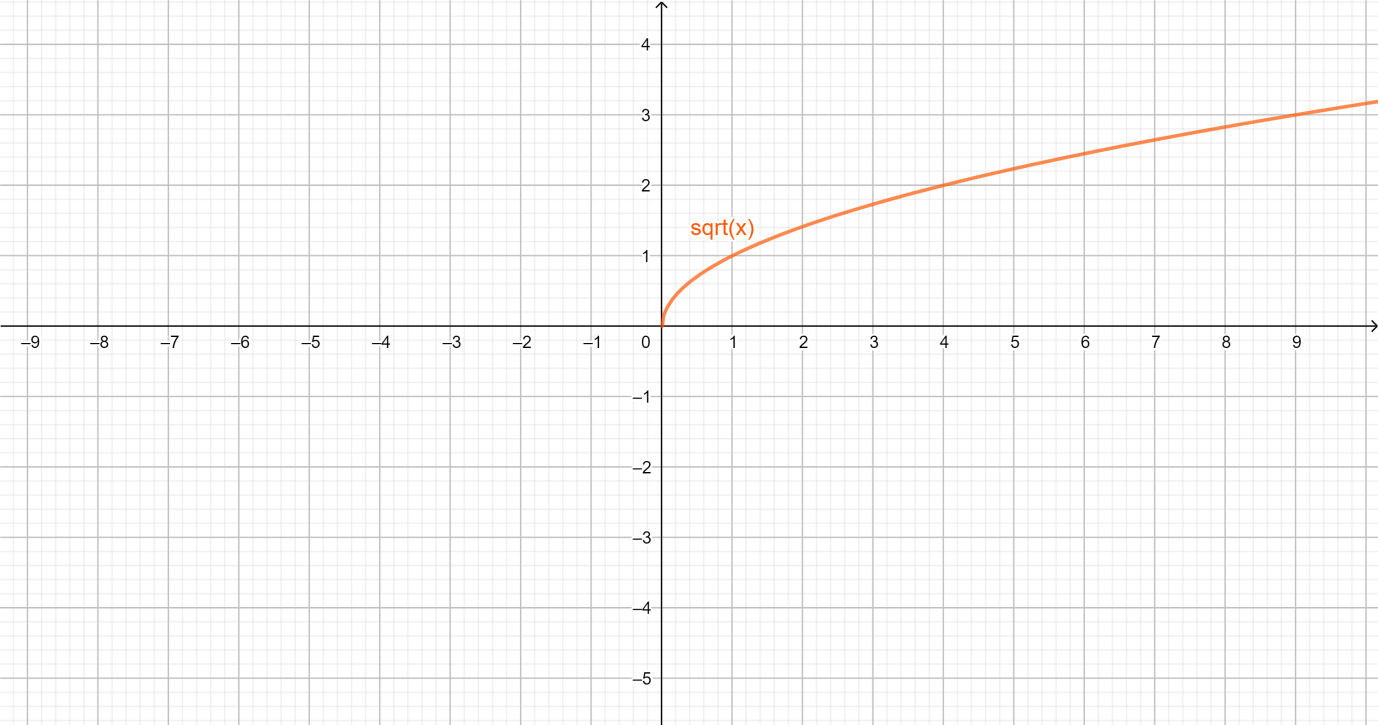
So here the graph of $ y = \sqrt x $ is the parent graph of $ y = \sqrt {x + 1} $ .
The parent graph is the graph of a relatively simple function. By transforming the function in various ways, the graph can be translated, reflected or otherwise changed.
In this problem, the parent graph is $ y = \sqrt x $ . And $ y = \sqrt {x + 1} $ is the same graph but when we compare it to the parent graphing it moves one unit to the left.
The domain of the function is when the term inside the square root is greater than or equal to zero. Let’s find this by solving the following inequality.
$ \Rightarrow x + 1 \geqslant 0 $
Adding $ - 1 $ to both sides of the above inequality, we get
$ \Rightarrow x + 1 - 1 \geqslant - 1 $ , cancelling $ - 1 $ and $ + 1 $ in the left hand side of the inequality, we get
$ \Rightarrow x \geqslant - 1 $

So, our domain is $ \left\{ {\left. x \right|x \geqslant - 1} \right\} $ and range is $ y \in R \geqslant 0 $

Note: The range of the parent graph $ y = \sqrt x $ is all real positive numbers and zero and a move to the left does nothing to change that. So the range of this function is also all the positive real numbers and zero, that is $ R \geqslant 0 $ .