Question

How do you graph $y = {\log _3}\left( {x - 2} \right)$?

Answer 1

Hint: To solve this question, we need to follow some certain steps. First, we need to find asymptotes for the given functions. In the next step we need to find three points on the graph. This can be done by using different values of $x$ greater than the asymptote and then by putting them into the given function.

Complete step by step solution:
We are given the function $y = {\log _3}\left( {x - 2} \right)$.
First, we will find the asymptotes of the function. This means that we need to find where the given function cannot be defined.
We know that the logarithm of the number exists only if the number is greater than zero.
Therefore, for the given function $y = {\log _3}\left( {x - 2} \right)$, we can say that the function cannot be defined for the values of $x$ less than or equal to 2 which is $x \leqslant 2$.
Therefore, for vertical asymptotes for the given function is $x = 2$.
Now, we will find the point where $x = 3$.
$y = {\log _3}\left( {x - 2} \right)$
We will now put $x = 3$.
$ \Rightarrow y = {\log _3}\left( {3 - 2} \right) = {\log _3}1 = 0$
Therefore, the y-intercept of the function is $\left( {3,0} \right)$.
Now, let us find the point where $x = 5$.
$y = {\log _3}\left( {x - 2} \right)$
We will now put $x = 5$.
$ \Rightarrow y = {\log _3}\left( {5 - 2} \right) = {\log _3}3 = 1$
Therefore, we get a point $\left( {5,1} \right)$on the graph.
Now, let us find the point where $x = 11$.
$ \Rightarrow y = {\log _3}\left( {11 - 2} \right) = {\log _3}9 = {\log _3}{3^2} = 2{\log _3}3 = 2\left( 1 \right) = 2$
Thus, we get another point $\left( {11,2} \right)$ on the graph.
Now we have three points $\left( {3,0} \right)$, $\left( {5,1} \right)$and $\left( {11,2} \right)$ and the vertical asymptotes $x = 2$. By using this information, we can get the graph of the function $y = {\log _3}\left( {x - 2} \right)$ as:

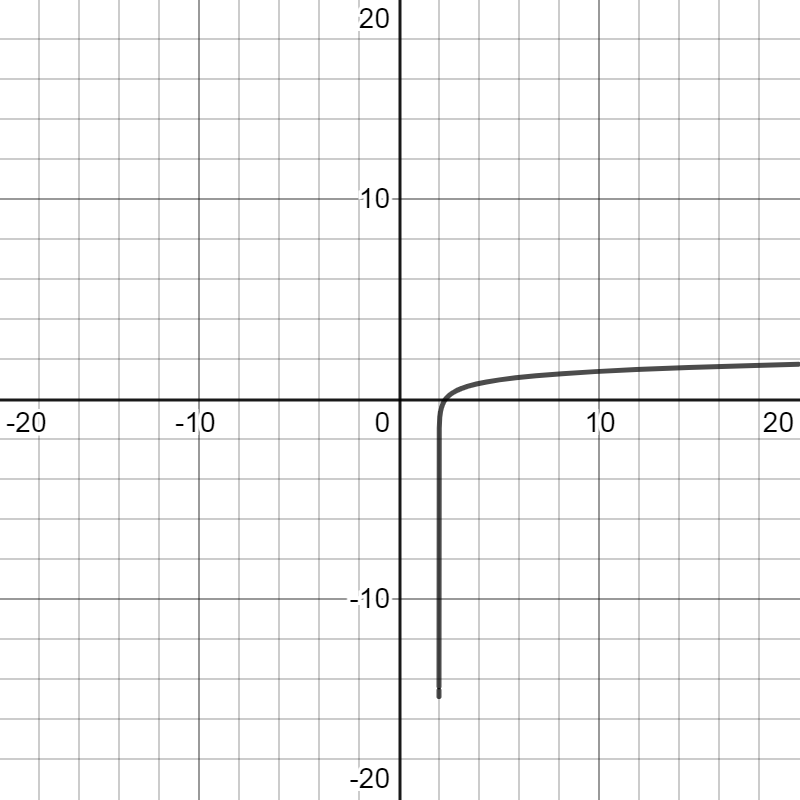
Note: Here, we have taken the values of $x$ to obtain the points $\left( {3,0} \right)$, $\left( {5,1} \right)$and $\left( {11,2} \right)$ such that they are in the relation with the base. As a result we have used two important properties of logarithm. First, ${\log _a}1 = 0$ , second the exponent rule, ${\log _a}{m^n} = n{\log _a}m$ and third ${\log _a}a = 1$.