
How do you graph $y = 1 + \sin \left( {\dfrac{1}{2}x} \right)$?
Answer
554.1k+ views
Hint: The given function is $y = 1 + \sin \left( {\dfrac{1}{2}x} \right)$
Use the form $a\sin (bx - c) + d$ to find the variables used to find the amplitude, period, phase shift and vertical shift.
We find the $x$ point, put $0,\pi ,2\pi ,3\pi ,4\pi $
Finally we get the result. And to draw a graph
Complete step-by-step solution:
The given function is $y = 1 + \sin \left( {\dfrac{1}{2}x} \right)$
We rewrite the function $y = \sin \left( {\dfrac{1}{2}x} \right) + 1$
Use the form $a\sin (bx - c) + d$ to find the variables used to find the amplitude, period, phase shift and vertical shift.
$a = 0$
$b = \dfrac{1}{2}$
$c = 0$
$d = 1$
Find the amplitude$\left| a \right|$
Amplitude: $1$
Find the period using the formula$\dfrac{{2\pi }}{{\left| b \right|}}$
The period of the function can be calculated using $\dfrac{{2\pi }}{{\left| b \right|}}$
Replace $b$ with $\dfrac{1}{2}$ in the formula for period.
Period$\dfrac{{2\pi }}{{\left| {\dfrac{1}{2}} \right|}}$
We solve the equation:
$\dfrac{1}{2}$ is approximately $0.5$ which is positive so remove the absolute value
Period:$\dfrac{{2\pi }}{{\dfrac{1}{2}}}$
Multiply the numerator by the reciprocal of the denominator, $2\pi \times 2$
Multiply $2$ by2, $4\pi $
Find the phase shift using the formula $\dfrac{c}{b}$.
Replace the values of $c$ and $b$ in the equation for phase shift.
$ \Rightarrow \dfrac{0}{{\dfrac{1}{2}}}$
Zero divide by anything the number is zero, hence we get
$0$
The vertical shift $d$ is $1$
List the properties of the trigonometric function.
Amplitude: $1$
Period: $4\pi $
Phase shift: $0$
Vertical shift: $1$
Select a few points to graph.
Find the point at $x = 0$
$ \Rightarrow y = \sin \left( {\dfrac{1}{2}x} \right) + 1$
Replace the variable $x$ with the $0$ in the expression
$ \Rightarrow f(0) = \sin \left( {\dfrac{0}{2}} \right) + 1$
Divide $0$ by $2$, hence we get
$ \Rightarrow f(0) = \sin 0 + 1$
The$\sin 0$ value is $0$, hence we get
$ \Rightarrow f(0) = 0 + 1$
The zero terms vanish
$ \Rightarrow f(0) = 1$
Find the point at $x = \pi $
$ \Rightarrow f(\pi ) = \sin \left( {\dfrac{\pi }{2}} \right) + 1$
The$\sin \left( {\dfrac{\pi }{2}} \right)$value is$1$
$ \Rightarrow f(\pi ) = 1 + 1$
Add$1$and$1$
$ \Rightarrow f(\pi ) = 2$
Find the point at $x = 2\pi $
$ \Rightarrow f(2\pi ) = \sin \left( {\dfrac{{2\pi }}{2}} \right) + 1$
Cancel the common factor, hence we get
$ \Rightarrow f(2\pi ) = \sin \left( \pi \right) + 1$
The$\sin \left( \pi \right)$ value is $0$
$ \Rightarrow f(2\pi ) = 0 + 1$
Add $0$ and$1$
$ \Rightarrow f(2\pi ) = 1$
Find the point at $x = 3\pi $
$ \Rightarrow f(3\pi ) = \sin \left( {\dfrac{{3\pi }}{2}} \right) + 1$
Apply the reference angle by finding the angle with equivalent trig values in the first quadrant. Make the expression negative because sine is negative in the fourth quadrant.
Cancel the common factor, hence we get
$ \Rightarrow f(3\pi ) = - \sin \left( {\dfrac{\pi }{2}} \right) + 1$
The$\sin \left( {\dfrac{\pi }{2}} \right)$value is$1$
$ \Rightarrow f(3\pi ) = - 1 \times 1 + 1$
Multiply $ - 1$ by $1$
$ \Rightarrow f(3\pi ) = - 1 + 1$
Subtract $ - 1$ by $1$
$ \Rightarrow f(3\pi ) = 0$
Find the point at $x = 4\pi $
$ \Rightarrow f(4\pi ) = \sin \left( {\dfrac{{4\pi }}{2}} \right) + 1$
Cancel the common factor, hence we get
$ \Rightarrow f(4\pi ) = \sin \left( {2\pi } \right) + 1$
The$\sin \left( {2\pi } \right)$value is$0$
$ \Rightarrow f(4\pi ) = 0 + 1$
Add $0$ and $1$
$ \Rightarrow f(4\pi ) = 1$
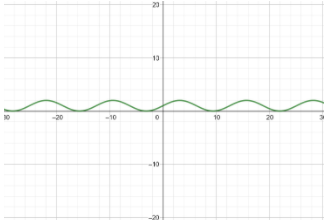
Note: The sine and cosine functions are useful for one very important reason, since they repeat in a regular pattern. There are vast arrays of things in and around us that repeat periodically. For example, the rising and setting of the sun, the motion of a spring up and down, the tides of the ocean and so on, are repeating at regular intervals of time. All periodic behavior can be studied through combinations of the sine and cosine functions.
Periodic functions are used throughout science to describe oscillations, waves and other phenomena that occur periodically.
Use the form $a\sin (bx - c) + d$ to find the variables used to find the amplitude, period, phase shift and vertical shift.
We find the $x$ point, put $0,\pi ,2\pi ,3\pi ,4\pi $
Finally we get the result. And to draw a graph
Complete step-by-step solution:
The given function is $y = 1 + \sin \left( {\dfrac{1}{2}x} \right)$
We rewrite the function $y = \sin \left( {\dfrac{1}{2}x} \right) + 1$
Use the form $a\sin (bx - c) + d$ to find the variables used to find the amplitude, period, phase shift and vertical shift.
$a = 0$
$b = \dfrac{1}{2}$
$c = 0$
$d = 1$
Find the amplitude$\left| a \right|$
Amplitude: $1$
Find the period using the formula$\dfrac{{2\pi }}{{\left| b \right|}}$
The period of the function can be calculated using $\dfrac{{2\pi }}{{\left| b \right|}}$
Replace $b$ with $\dfrac{1}{2}$ in the formula for period.
Period$\dfrac{{2\pi }}{{\left| {\dfrac{1}{2}} \right|}}$
We solve the equation:
$\dfrac{1}{2}$ is approximately $0.5$ which is positive so remove the absolute value
Period:$\dfrac{{2\pi }}{{\dfrac{1}{2}}}$
Multiply the numerator by the reciprocal of the denominator, $2\pi \times 2$
Multiply $2$ by2, $4\pi $
Find the phase shift using the formula $\dfrac{c}{b}$.
Replace the values of $c$ and $b$ in the equation for phase shift.
$ \Rightarrow \dfrac{0}{{\dfrac{1}{2}}}$
Zero divide by anything the number is zero, hence we get
$0$
The vertical shift $d$ is $1$
List the properties of the trigonometric function.
Amplitude: $1$
Period: $4\pi $
Phase shift: $0$
Vertical shift: $1$
Select a few points to graph.
Find the point at $x = 0$
$ \Rightarrow y = \sin \left( {\dfrac{1}{2}x} \right) + 1$
Replace the variable $x$ with the $0$ in the expression
$ \Rightarrow f(0) = \sin \left( {\dfrac{0}{2}} \right) + 1$
Divide $0$ by $2$, hence we get
$ \Rightarrow f(0) = \sin 0 + 1$
The$\sin 0$ value is $0$, hence we get
$ \Rightarrow f(0) = 0 + 1$
The zero terms vanish
$ \Rightarrow f(0) = 1$
Find the point at $x = \pi $
$ \Rightarrow f(\pi ) = \sin \left( {\dfrac{\pi }{2}} \right) + 1$
The$\sin \left( {\dfrac{\pi }{2}} \right)$value is$1$
$ \Rightarrow f(\pi ) = 1 + 1$
Add$1$and$1$
$ \Rightarrow f(\pi ) = 2$
Find the point at $x = 2\pi $
$ \Rightarrow f(2\pi ) = \sin \left( {\dfrac{{2\pi }}{2}} \right) + 1$
Cancel the common factor, hence we get
$ \Rightarrow f(2\pi ) = \sin \left( \pi \right) + 1$
The$\sin \left( \pi \right)$ value is $0$
$ \Rightarrow f(2\pi ) = 0 + 1$
Add $0$ and$1$
$ \Rightarrow f(2\pi ) = 1$
Find the point at $x = 3\pi $
$ \Rightarrow f(3\pi ) = \sin \left( {\dfrac{{3\pi }}{2}} \right) + 1$
Apply the reference angle by finding the angle with equivalent trig values in the first quadrant. Make the expression negative because sine is negative in the fourth quadrant.
Cancel the common factor, hence we get
$ \Rightarrow f(3\pi ) = - \sin \left( {\dfrac{\pi }{2}} \right) + 1$
The$\sin \left( {\dfrac{\pi }{2}} \right)$value is$1$
$ \Rightarrow f(3\pi ) = - 1 \times 1 + 1$
Multiply $ - 1$ by $1$
$ \Rightarrow f(3\pi ) = - 1 + 1$
Subtract $ - 1$ by $1$
$ \Rightarrow f(3\pi ) = 0$
Find the point at $x = 4\pi $
$ \Rightarrow f(4\pi ) = \sin \left( {\dfrac{{4\pi }}{2}} \right) + 1$
Cancel the common factor, hence we get
$ \Rightarrow f(4\pi ) = \sin \left( {2\pi } \right) + 1$
The$\sin \left( {2\pi } \right)$value is$0$
$ \Rightarrow f(4\pi ) = 0 + 1$
Add $0$ and $1$
$ \Rightarrow f(4\pi ) = 1$
| $x$ | $f(x)$ |
| $0$ | $1$ |
| $\pi $ | $2$ |
| $2\pi $ | $1$ |
| $3\pi $ | $0$ |
| $4\pi $ | $1$ |

Note: The sine and cosine functions are useful for one very important reason, since they repeat in a regular pattern. There are vast arrays of things in and around us that repeat periodically. For example, the rising and setting of the sun, the motion of a spring up and down, the tides of the ocean and so on, are repeating at regular intervals of time. All periodic behavior can be studied through combinations of the sine and cosine functions.
Periodic functions are used throughout science to describe oscillations, waves and other phenomena that occur periodically.
Recently Updated Pages
Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 12 Business Studies: Engaging Questions & Answers for Success

Trending doubts
What are the major means of transport Explain each class 12 social science CBSE

Draw the diagram showing the germination of pollen class 12 biology CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

RNA and DNA are chiral molecules their chirality is class 12 chemistry CBSE

Draw a neat and well labeled diagram of TS of ovary class 12 biology CBSE

What is Saheb looking for in the garbage dump Where class 12 english CBSE




