Question

How do you graph using the intercepts for $ - x - 7y = 14$

Answer 1

Hint: First we find the axis intercept values in the given equation. Also, when it is either $x$ or $y$ values are $0$. Then we have to plot the intercepts for the given equation in the graph. Finally we get the required solution.

Complete step-by-step solution:
It is given that the question we have to find the $x - $ intercept and $y - $ intercept for the straight line: $ - x - 7y = 14$
Before we start solving this question, let us see what the $x - $ intercept and the $y - $ intercept which is also known as horizontal intercept and vertical intercept by putting $x = 0{\text{, y = 0 }}$ for each one respectively.
Our equation is linear function; the two intercepts can be calculated as follows:
Substituting $x = 0$ in the given equation ie., $ - x - 7y = 14$
$ \Rightarrow - (0) - 7y = 14$
On rewriting we get,
$ \Rightarrow - 7y = 14$
On dividing \[ - 7\] on both sides we get,
$ \Rightarrow y = \dfrac{{14}}{{ - 7}}$
Let us divide the term and we get,
$ \Rightarrow y = - 2$
Hence we get the $x - $ intercept value.
$\therefore $$x - $ Intercept is $y = - 2$
Also, we need to find $y - $ intercept.
Now we are substitute, $y = 0$ in the given equation,
$ \Rightarrow - x - 7y = 14$
On putting the value of zero in place of $y.$
 $ \Rightarrow - x - 7(0) = 14$
Multiplying $7$ by $0$ we get
$ \Rightarrow - x - 0 = 14$
By using the elementary operation, we get
$ \Rightarrow - x = 14$
Dividing the whole number $14$ by $( - 1)$, we get
$ \Rightarrow x = - 14$
$\therefore y - $Intercept is $x = - 14$.
Hence, we get $\therefore $$x - $ Intercept is $y = - 2$
$\therefore y - $ Intercept is $x = - 14$.

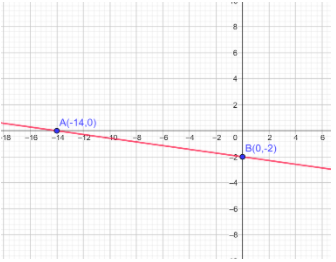
Note: $x - $ intercept is a point at which the graph intersects $x - axis$. That means we always have $y$ equal to zero Similarly we can say that for the $y - $intercept is a point at which the graph intersects $y - axis.$ That means we always have $x$ equal to zero in the coordinate system.
We have to know about the concept of $x - $ intercept and $y - $ intercept for a straight line, satisfying the condition of $x = 0{\text{ and y = 0}}$ in the equation of the given line.