Question

How do you graph using the intercepts for \[2x+y=13\] ?

Answer 1

Hint: In order to graph plot for the equation, \[2x+y=13\] , we need the points to be plotted in the graph, however here, we need to draw using the intercepts , for this, we can find the two intercepts , \[x-\] and \[y-\] intercepts by putting \[x\] and \[y\] zero one by one and then simply plotting the intercepts.

Complete step-by-step answer:
Firstly let us write the equation, for which we need to plot the graph
 \[2x+y=13\]
Let us find the \[x-\] and \[y-\] intercepts
Now, to find the \[x-\] intercept, put \[y=0\] in the equation
i.e.
  \[
   2x+y=13 \\
  \Rightarrow 2x+0=13 \\
  \Rightarrow 2x=13 \\
  \Rightarrow x=\dfrac{13}{2} \;
\]
Therefore, the \[x-\] intercept is \[\dfrac{13}{2}\]
Now, let us find the \[y-\] intercept
For this, let us put \[x=0\] in the equation
 \[
   2x+y=13 \\
  \Rightarrow 2\left( 0 \right)+y=13 \\
  \Rightarrow y=13 \;
\]
Thus, we get the \[y-\] intercept, which is \[13\]
Therefore, we get the intercept points as
 \[\left( \dfrac{13}{2},0 \right)\] and \[\left( 0,13 \right)\]
Now, if we plot these two points in the graph, we get

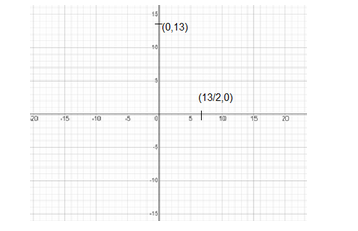
Now, this equation is for a straight line graph for which the intercepts have been drawn
If we join the two points, we get the graph as required

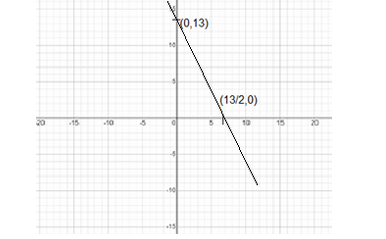
Hence, the graph is plotted.

Note: The formula used for the graph is for finding the intercepts. For finding \[x-\] intercept, first put \[y=0\] in the equation and in order to find the \[y-\] intercept, put \[x=0\] , in this way the two points for the graph are found and then plotted to get a straight line graph.