Question

How do you graph using slope and intercept form $ y=\dfrac{1}{4}x-1 $ ?

Answer 1

Hint: In the given question, we have been asked to draw a graph using the slope and intercept form of the equation. We have given an equation of a line as $ y=\dfrac{1}{4}x-1 $ , we have to write the slope-intercept of the given line which represented as $ y=mx+c $ where $ m $ is the slope of the line and $ c $ is the y-intercept and $ \dfrac{-c}{m} $ is the x-intercept. By getting the x-intercept and the y-intercept, we will connect these two points in the graph and in this way we will get the required graph.
Formula used:
The equation of the line in the slope and intercept form is given by;
 $ y=mx+c $
Where,
 $ m $ is the slope of the line and $ c $ is the y-intercept and $ \dfrac{-c}{m} $ is the x-intercept.

Complete step by step solution:
We have equation of line,
 $ y=\dfrac{1}{4}x-1 $
Rewrite the above equation as,
 $ y=\dfrac{1}{4}x+\left( -1 \right) $
Now,
We compare the given equation with the general linear equation i.e., $ y=mx+c $
Hence,
Slope of the given line, $ m=\dfrac{1}{4} $ .
Y-intercept of the given line, $ c=-1 $ .
Therefore, we can say that point $ (0,-1) $ lies on the line.
X-intercept of the given line, $ \dfrac{-c}{m}=-\dfrac{-1}{\dfrac{1}{4}}=1\times \dfrac{4}{1}=4 $ .
Therefore, we can say that point $ (4,0) $ lies on the line.
With the help of two points, we can plot the graph by connecting the points as follow,

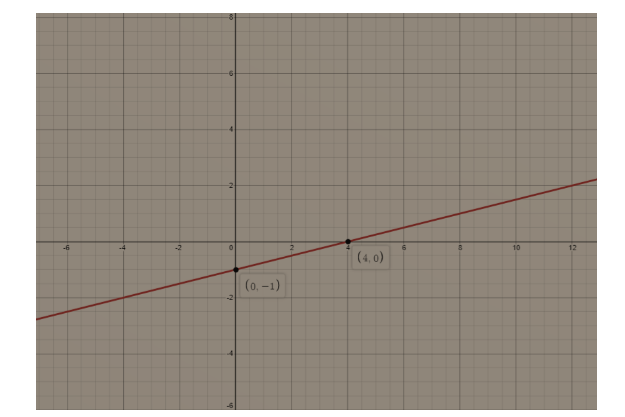
Note: In this question, it is important to note here that $ y=mx+c $ is called the slope-intercept form of the equation of the line. This type of linear equation is sometimes called a slope-intercept form because we can easily find the slope and the intercept of the corresponding lines. This also allows us to graph it. We can quickly tell the slope i.e., $ m $ , the y-intercepts i.e., $ (y,0) $ and the x-intercept i.e., $ (0,y) $ . And then we can graph the corresponding line by connecting the two lines.