Question

How do you graph the number $ 7 - 5i $ in the complex plane and find its absolute value?

Answer 1

Hint: We have been given a complex number. We have to plot this number as a point in the complex plane. A complex plane is a coordinate system where one axis represents the real part and the other axis represents the imaginary part. The absolute value of a complex number $ \left( {a + bi} \right) $ can be found using the formula $ \sqrt {{a^2} + {b^2}} $ .

Complete step by step solution:
We have to plot the complex number $ 7 - 5i $ in the complex plane.
A complex plane is a coordinate system with x-axis representing the real part and the y-axis representing the imaginary part.
To find the real and the imaginary part, we compare the given complex number with $ a + bi $ .
In a complex number, the terms associated with $ i $ is the imaginary part, and the other term is the real part, i.e. $ a $ is the real part and $ b $ is the imaginary part. Thus, the coordinates of the complex number $ \left( {a + bi} \right) $ is $ \left( {\operatorname{Re} (z),\;\operatorname{Im} (z)} \right) $ or $ \left( {a,\;b} \right) $ .
Let us represent the given complex number as $ z = 7 - 5i $ .
Here the real part of $ z $ , denoted as $ \operatorname{Re} (z) $ , is $ 7 $ . And the imaginary part of $ z $ , denoted as $ \operatorname{Im} (z) $ , is $ - 5 $ .
Now we plot the number. For this we have to plot the coordinate $ \left( {7,\; - 5} \right) $ on the complex plane.
This is as shown below by point A,

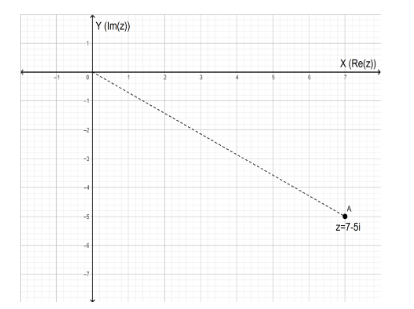
Now we have to find the absolute value of the given complex number.
For a complex number $ z = \left( {a + bi} \right) $ , the absolute value is given as $ \left| z \right| = \sqrt {{a^2} + {b^2}} $ .
Thus the absolute value of the given complex number $ 7 - 5i $ is $ \sqrt {{a^2} + {b^2}} = \sqrt {{7^2} + {{\left( { - 5} \right)}^2}} = \sqrt {49 + 25} = \sqrt {74} \approx 8.602 $

Note: We plotted the given complex number simply as a coordinate point on the complex plane where the coordinates are taken as $ \left( {\operatorname{Re} (z),\;\operatorname{Im} (z)} \right) $ . Notice that the formula for absolute value is similar to that of the distance formula. In a way, the absolute value represents the distance between the origin and the point representing the complex number on the graph.