Question

How do you graph the given function ${{\left( x-3 \right)}^{2}}+{{\left( y-2 \right)}^{2}}=9$?

Answer 1

Hint: We start solving the problem by making the necessary arrangements in the given equation. We then make use of the fact that the equation ${{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{r}^{2}}$ represents the circle with its centre at $\left( a,b \right)$ and radius r units to find the centre and radius. We then plot the obtained centre in the graph and then draw a circle of radius 3 units with the point we just plotted as centre to complete plotting the given function.

Complete step by step answer:
According to the problem, we are asked to plot the graph of the given function ${{\left( x-3 \right)}^{2}}+{{\left( y-2 \right)}^{2}}=9$.
We have given the equation ${{\left( x-3 \right)}^{2}}+{{\left( y-2 \right)}^{2}}=9$.
$\Rightarrow {{\left( x-3 \right)}^{2}}+{{\left( y-2 \right)}^{2}}={{3}^{2}}$ ---(1).
From equation (1), we can see that the obtained equation resembles ${{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{r}^{2}}$. We know that the equation ${{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{r}^{2}}$ represents the circle with its centre at $\left( a,b \right)$ and radius r units. Using this fact, we get the centre and radius of the circle ${{\left( x-3 \right)}^{2}}+{{\left( y-2 \right)}^{2}}={{3}^{2}}$ as $\left( 3,2 \right)$ and 3 units.
Now, let us represent the point $\left( 3,2 \right)$ on the graph as shown below:

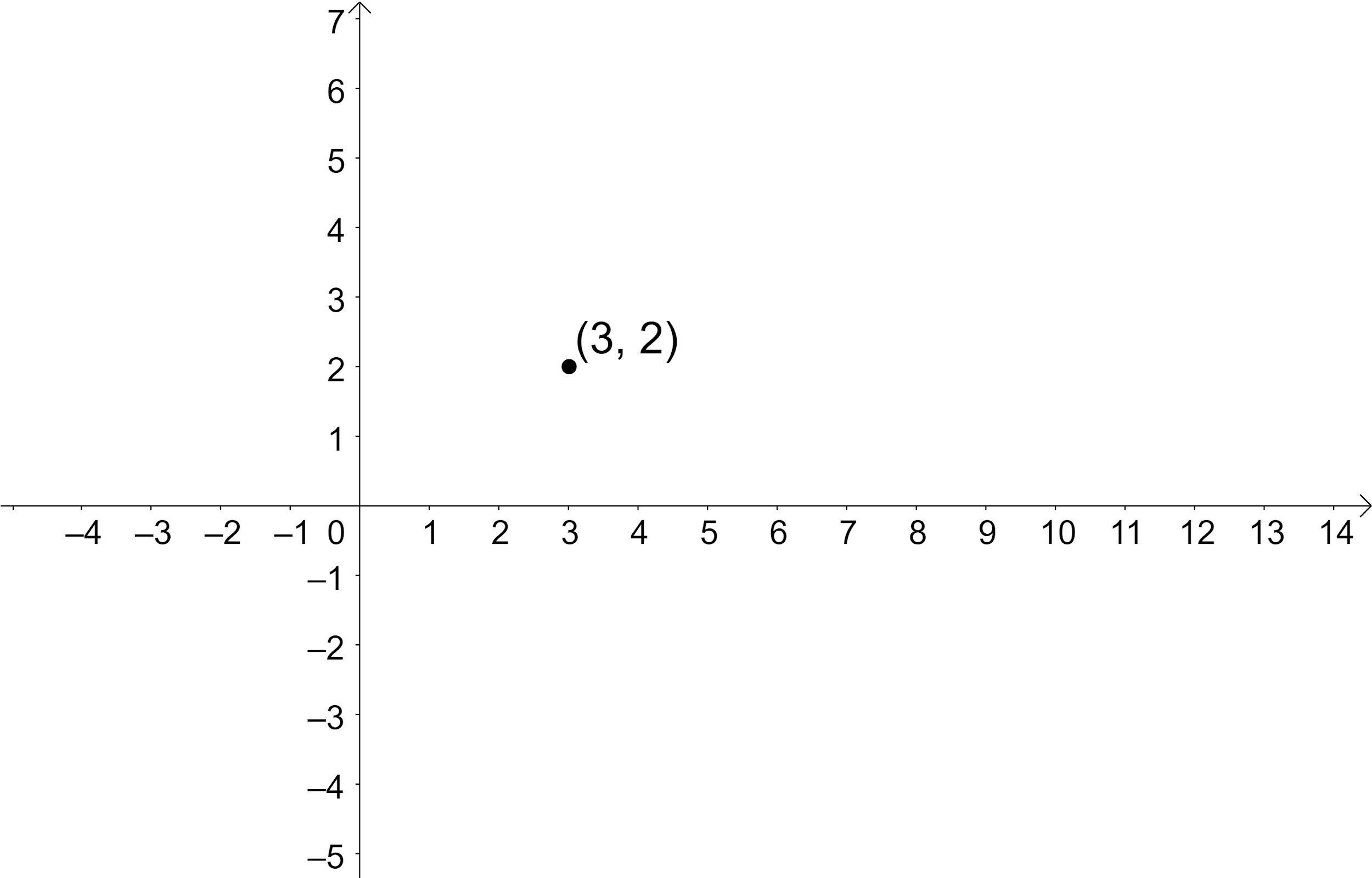
Now, let us draw a circle of 3 units taking the point $\left( 3,2 \right)$ as the centre which is the required plot.

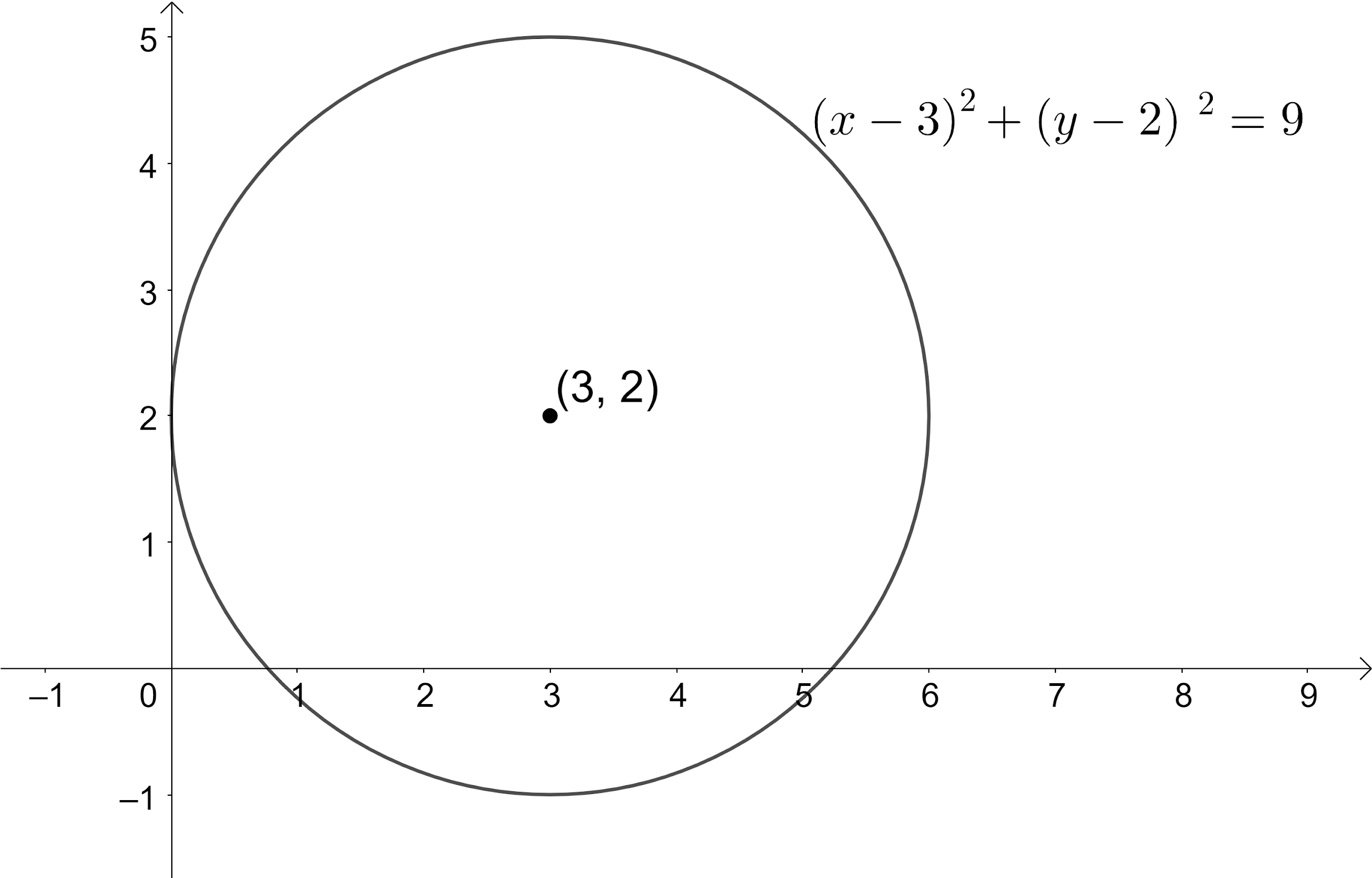
Note:
Whenever we get this type of problem, we first try to find the figure that the given equation represents to get the required plot. We can also plot the given function by finding any points on the curve and then drawing it. We should not make calculation mistakes while finding the centre and radius of the given circle. Similarly, we can expect problems to plot the given function ${{x}^{2}}+{{y}^{2}}+x+y=0$.