Question

How do you graph \[3x - 2y = 6\] by plotting intercepts?

Answer 1

Hint: To graph an equation, we must find x and y intercepts. The x-intercepts are the points at which the graph crosses the x-axis. To find the x-intercept, set y = 0 and solve for x, to find the y-intercept, set x = 0 and solve for y, hence we get the x and y intercepts by solving and to graph a line, graph the points if they exist, and then connect the two points with a straight line.

Complete step-by-step answer:
Let us write the given linear equation:
  \[3x - 2y = 6\]
To graph the solution for the given equation, we need to find x and y intercepts.
Let us find the x-intercepts: To find the x-intercept, set y = 0 and solve for x i.e.,
 \[3x - 2y = 6\]
 \[3x - 2\left( 0 \right) = 6\]
 \[ \Rightarrow \] \[3x = 6\]
Divide both sides of the equation by 3 to get the value of x as
 \[\dfrac{{3x}}{3} = \dfrac{6}{3}\]
 \[ \Rightarrow \] \[x = \dfrac{6}{3}\]
We get the value of x as,
 \[x = 2\]
Hence, the x-intercept of the given equation is \[\left( {2,0} \right)\] .
Now let us find the y-intercepts: To find the y-intercept, set x = 0 and solve for y i.e.,
 \[3x - 2y = 6\]
 \[3\left( 0 \right) - 2y = 6\]
 \[ - 2y = 6\]
Divide both sides of the equation by 2 to get the value of y as
 \[\dfrac{{ - 2y}}{2} = \dfrac{6}{2}\]
 \[ \Rightarrow \] \[ - y = \dfrac{6}{2}\]
The value of y is,
 \[ \Rightarrow \] \[y = - 3\]
Hence, the y-intercept of the given equation is \[\left( {0, - 3} \right)\] .
Now, let us graph the solution: To graph this line using the intercepts, first graph the two points as shown A = \[\left( {2,0} \right)\] and B = \[\left( {0, - 3} \right)\] ,then connect the two points with a straight line.

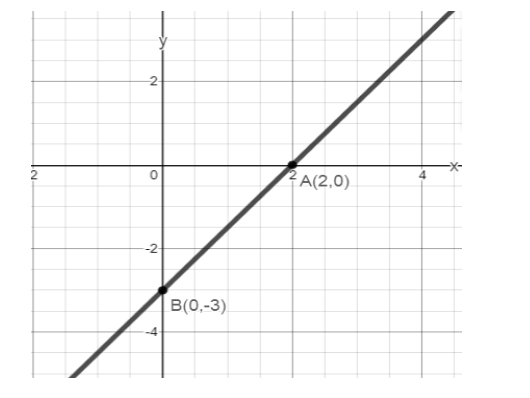
Note: The graph passes through the y axis, x=0 and graph pass through the x axis, y=0 and when we are finding x-intercept y-coordinate is zero and vice versa then solve for x and y intercepts and any line can be graphed using two points i.e., select two x values, and plug them into the equation to find the corresponding y values and graph the solution such that the x-intercept is along x-axis and y-intercept is along y-axis.