Question

How do you graph $2x-y=6$ using intercepts?

Answer 1

Hint: Change of form of the given equation will give the x-intercept and y-intercept of the line $2x-y=6$. We change it to the form of $\dfrac{x}{p}+\dfrac{y}{q}=1$ to find the x intercept, and y intercept of the line as $p$ and $q$ respectively. then we place the points on the axes and from there we draw the line on the graph.

Complete step-by-step solution:
We are taking the general equation of line to understand the slope and the intercept form of the line $2x-y=6$. It’s in the form of $ax+by=c$. We convert it to $y=2x-6$. The equation is in the form of $y=mx+k$. m is the slope of the line. The slope of the line is 2.
We have to find the x-intercept, and y-intercept of the line $2x-y=6$.
For this we convert the given equation into the form of $\dfrac{x}{p}+\dfrac{y}{q}=1$. From the form we get that the x intercept, and y intercept of the line will be$p$ and $q$ respectively. The points will be $\left( p,0 \right),\left( 0,q \right)$.
The given equation is $2x-y=6$. Converting into the form of $\dfrac{x}{p}+\dfrac{y}{q}=1$, we get
\[\begin{align}
  & 2x-y=6 \\
 & \Rightarrow \dfrac{2x}{6}-\dfrac{y}{6}=1 \\
 & \Rightarrow \dfrac{x}{3}+\dfrac{y}{-6}=1 \\
\end{align}\]
Therefore, the x intercept, and y intercept of the line $2x-y=6$ is 3 and 6 respectively. The axes intersecting points are $\left( 3,0 \right),\left( 0,-6 \right)$.

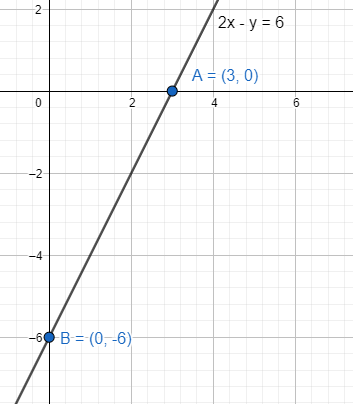
Note: A line parallel to the X-axis does not intersect the X-axis at any finite distance. Hence, we cannot get any finite x-intercept of such a line. Same goes for lines parallel to the Y-axis. In case of slope of a line the range of the slope is 0 to $\infty $.