Question

How do you graph $2x + 3y > 4$ in coordinate plane?

Answer 1

Hint: Here we can express the inequality bringing all the terms involving a variable on the left and all the terms involving the other variable on the right. It is easy to draw a graph.

Complete step by step answer:
Now we are going to express the inequality bringing all the terms involving a variable on the left and all the terms involving a variable on the left, and all the terms involving the other variable on the right. In the end, we will have an inequality of the form $y \leqslant f(x)$ or $y \geqslant f(x)$ . And this is easy to graph, because if we can draw the graph of $f(x)$ . Then we will have that $y \leqslant f(x)$ represents all the area under the function $f$, and $y \geqslant f(x)$ ,of course, the area over the function.
Consider the given inequality, $2x + 3y > 4$
In this form it would be very hard to say which points satisfy the inequality, but with some manipulations as we obtain
Move the $2x$ to the other side to get $3y > - 2x + 4$
Then divide by $3$ to get $y > - \dfrac{2}{3}x + \dfrac{4}{3}$ .
From here, graph the line $y > - \dfrac{2}{3}x + \dfrac{4}{3}$. Then the shade in the area which satisfies the inequality. It is called a half plane because its area is half of the area of the entire plane. Also, make the line a dotted line to show that it is not included.
Now to find the boundary line for the inequality,
Solve for two points as an equation instead of an inequality to find the boundary line for the inequality.
The given equation becomes$y = - \dfrac{2}{3}x + \dfrac{4}{3}$
Put $x = 0$ in the above equation,
$y = - \dfrac{2}{3}(0) + \dfrac{4}{3}$
$ \Rightarrow y = \dfrac{4}{3}$
$\therefore $ The coordinate is $\left( {0,\dfrac{4}{3}} \right)$
Put $y = 0$ in the above equation,
$ \Rightarrow 0 = - \dfrac{2}{3}x + \dfrac{4}{3}$
Taking LCM and then cross multiplying,
$ \Rightarrow 0 = - 2x + 4$
 On equating,
$ \Rightarrow - 2x = - 4$
Keeping variable on the left hand side
$ \Rightarrow x = \dfrac{4}{2}$
On dividing, we get
$ \Rightarrow x = 2$
$\therefore $ The coordinate is $\left( {2,0} \right)$
We can now graph the two points on the coordinate plane and draw a line through the points to mark the boundary of the inequality.
The graph of $2x + 3y > 4$ and the points $A = \left( {0,\dfrac{4}{3}} \right)$ and $B = \left( {2,0} \right)$,

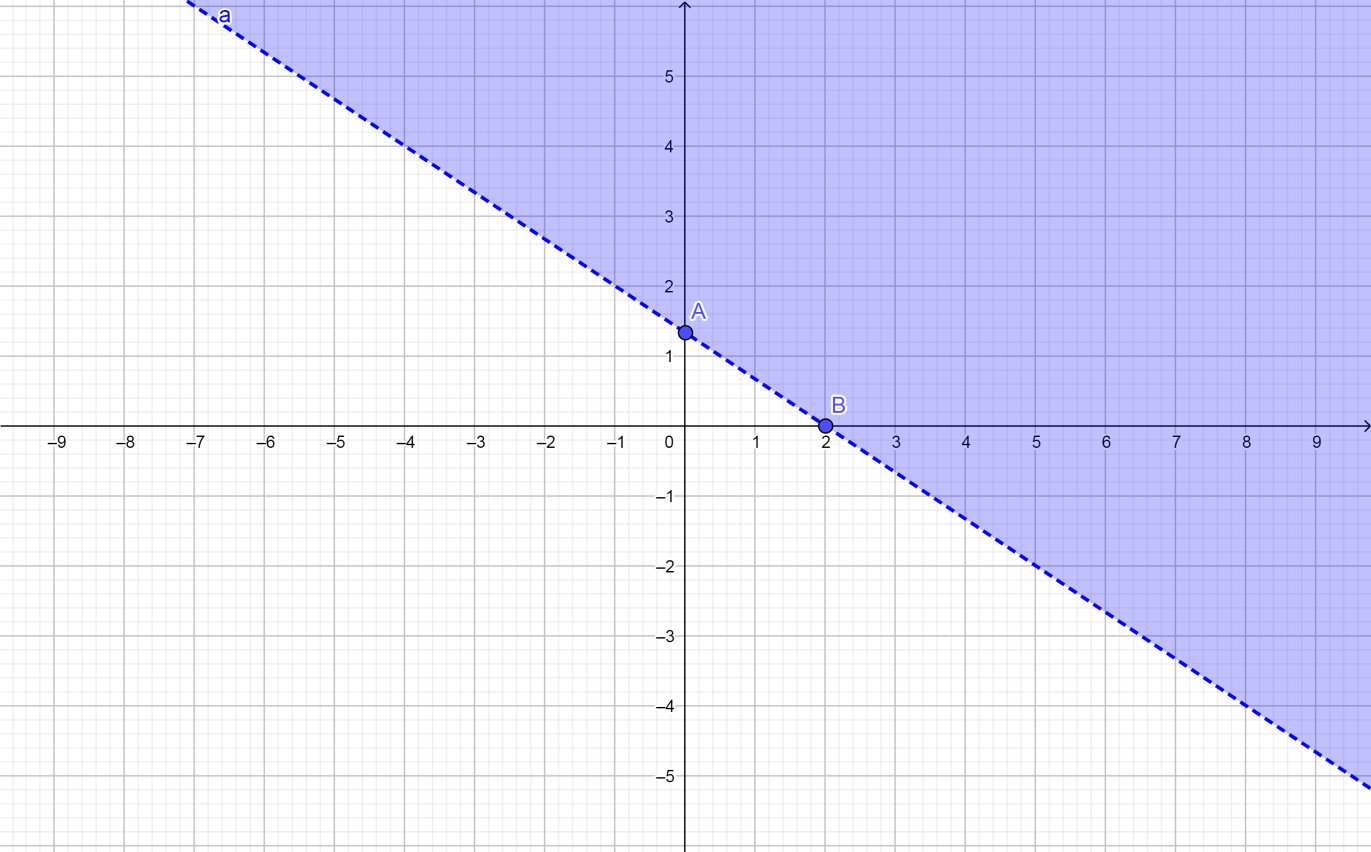
Note: If you have $y < f(x)$ the graph of the function $f$ is not included.
 Since it represents the points for which $y = f(x)$.
Here we have $y = f(x) = - \dfrac{2}{3}x + \dfrac{4}{3}$ which is a line and so it is very easy to graph.
Once graphed, we need to consider all the portions of the plane above the line to solve your inequality.