Question

Given triangle ABC with medians AE , BF , CD , FH parallel and equal in length to AE ; BH and HE are drawn ; FE extended meets BH in G . Which one of the following statements is not necessarily correct?

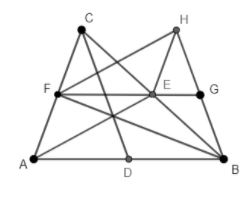
(a) AFHE is a parallelogram
(b) HE = HG
(c) BH = DC
(d) \[\text{FG=}\dfrac{3}{4}\text{AB}\]

Answer 1

Hint: To solve this question we will check each and every option . And in this question a construction is needed which is we have to extend line segment HE to meet line segment AB . And in this question you have to use the midsegment theorem and properties of median and properties of parallelogram which is that opposite sides are equal and parallel of a parallelogram .

Complete step-by-step answer:
In the above question the given figure is -

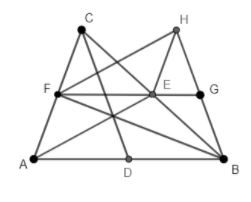
Other information which is given in the question is CD , BF , AE are medians of AB , BC and CD respectively .And FH is parallel and equal to AE .

Since FH is parallel and equal to AE
And any Quadrilateral having one pair of opposite sides are parallel and equal , then it is a parallelogram.
\[\Rightarrow \]AFHE is a parallelogram.
\[\Rightarrow \]option (a) is true.
Construction: - Now , we have to extend the line segment HE to meet the line segment AB.

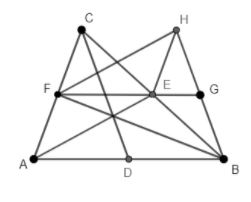
Now,
The line joining the midpoints of two sides of the triangle is called midsegment.
And according to the midsegment theorem it states that the midsegment connecting the midpoints of two sides of a triangle is parallel to the third side of the triangle, and the length of this midsegment is half of the length of the third side.
\[\Rightarrow \]FE is parallel to AB or AD \[...(i)\]
And as AFHE is a parallelogram
\[\Rightarrow \]AF is parallel to HE or HD \[...(ii)\]
By using equation (i) and (ii), we can say that -
\[\Rightarrow \]AFED is a parallelogram
\[\Rightarrow \]AF = DE \[...(iii)\]
And as AFHE is a parallelogram
\[\Rightarrow \]AF = HE \[...(iv)\]
And as F is the midpoint of AC
\[\Rightarrow \]AF = FC \[...(v)\]
Now,
AC = AF + FC
\[\Rightarrow \]AC = 2AF (Using \[(v)\] )
\[\Rightarrow \]AC = AF + AF = DE + HE (Using \[(iii)\,and\,(iv)\] )
\[\Rightarrow \]AC = DH \[...(vi)\]
Now in \[\Delta ACD\,and\,\Delta DHB\]
AC=DH (Using \[(vi)\] )
And as AC is parallel to DH
\[\Rightarrow \]\[\angle CAD=\angle HDB\] ,as these angles are corresponding angles of these parallel lines.
And AD = DB ,since D is the midpoint of line segment AB.
\[\Rightarrow \]\[\Delta ACD\,and\,\Delta DHB\] are congruent triangles.

\[\Rightarrow \]BH = DC
\[\Rightarrow \]option (c) is true.
Now ,
FG = FE + EG
\[\Rightarrow FG=\dfrac{1}{2}AB+\dfrac{1}{2}DB\] ( Using midsegment theorems in \[\Delta ABC\,and\,\Delta HDB\] )
\[\Rightarrow FG=\dfrac{1}{2}AB+\dfrac{1}{2}\times \dfrac{1}{2}AB\] (As D is the midpoint of AB )
\[\Rightarrow FG=\dfrac{3}{4}AB\]
\[\Rightarrow \]option (d) is true.

So, the correct answer is “Option (d)”.

Note: Alternative method to prove the Option (d) is –
As AFED is a parallelogram
\[\Rightarrow \] FE = AD
And as D is the mid-point of AB
\[\Rightarrow \] AD = DB
\[\begin{align}
  & \Rightarrow FE=AD=DB \\
 & \Rightarrow FE=\dfrac{1}{2}AB \\
\end{align}\]
Similarly ,
\[EG=\dfrac{1}{2}DB\]
\[\Rightarrow EG=\dfrac{1}{2}\times \dfrac{1}{2}AB\]
\[\begin{align}
  & \Rightarrow FG=FE+EG \\
 & FG=\dfrac{1}{2}AB+\dfrac{1}{2}\times \dfrac{1}{2}AB \\
 & \Rightarrow FG=\dfrac{3}{4}AB \\
\end{align}\]