Question

Given the two ends of the latus rectum, the maximum number of parabolas that can be drawn is
A. 1
B. 2
C. 0
D. infinite

Answer 1

Hint: In mathematics, a parabola is a plane curve which is mirror-symmetrical and is approximately U-shaped. It fits several other superficially different mathematical descriptions, which can all be proved to define exactly the same curves.
One description of a parabola involves a point (the focus) and a line (the directrix). The focus does not lie on the directrix. The parabola is the locus of points in that plane that are equidistant from both the directrix and the focus.
The formula that gives the end points of the latus rectum of a parabola is as follows
\[(x,y)=(a,\pm 2a)\]
(Where the parabola is the standard one having the formula as \[{{y}^{2}}=4ax\] )
In such questions, one might get the answer diagrammatically.

Complete step-by-step answer:
As mentioned in the question, we have to find the maximum number of parabolas that can pass through a set of end points of a latus rectum.
Now, as mentioned in the hint, we will first make the possible diagram of the parabolas to get to the answer.

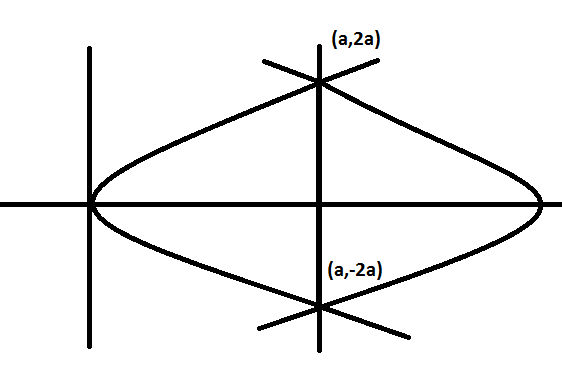
Now, as observed from the diagram, one can see that the maximum number of parabolas that can pass through the given coordinates of the end points of a latus rectum is 2.

Note: Another explanation for this answer is that
Since, the latus rectum and axis of parabola are perpendicular bisectors of each other.
So, the point where the latus rectum meets the axis of parabola bisects the latus rectum.Hence, there can be only two such parabolas.