Question

Given an equation of two sides of a square as $5x + 12y - 10 = 0$, $5x + 12y + 29 = 0$. Also given a point M (-3, 5) lying on one of its side then,
Number of possible squares are:
$\left( a \right)0$
$\left( b \right)1$
$\left( c \right)2$
$\left( d \right)3$

Answer 1

Hint – In this question first check whether the given lines are parallel or perpendicular to each other using slope concept then use the distance formula between two lines which is given as \[d = \dfrac{{\left| {{c_1} - {c_2}} \right|}}{{\sqrt {{a^2} + {b^2}} }}\], where $c_1$ and $c_2$ are the constants of the line so use these concepts to reach the solution of the question.

Complete step-by-step answer:

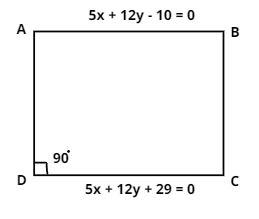
Given equations of two sides of a square is
$5x + 12y - 10 = 0$........... (1)
And
$5x + 12y + 29 = 0$............... (2)
As we know for linear equation ax + by + c = 0 the slope is the ratio of negative times x coefficient to coefficient of y.
So slope of equation (1) is
$ \Rightarrow {m_1} = \dfrac{{ - 5}}{{12}}$
And the slope of equation (2) is
$ \Rightarrow {m_2} = \dfrac{{ - 5}}{{12}}$
So as we see that both the slopes are the same therefore both lines are parallel to each other as shown in the above figure.
Now it is that point M (-3, 5) lying on one of its sides so suppose it is lying on the third side of the square.
Now as we know all the sides of the square are perpendicular to each other and are equal length.
So let us consider the square ABCD as shown above AB and CD sides’ represents lines $5x + 12y - 10 = 0$and $5x + 12y + 29 = 0$ respectively.
So the slope of line AD is perpendicular to line CD.
Let the slope of line AD be $m_3$.
$ \Rightarrow {m_2}{m_3} = - 1$
$ \Rightarrow {m_3} = \dfrac{{ - 1}}{{{m_2}}} = \dfrac{{ - 1}}{{\dfrac{{ - 5}}{{12}}}} = \dfrac{{12}}{5}$
Similarly the slope of side BC ($m_4$) = $\dfrac{{12}}{5}$
So the equation of line AD is
$12x - 5y + {c_1} = 0$
And equation of line BC is
$12x - 5y + {c_2} = 0$, (from the general equation of line $y = mx + c$, where m, $c_1$ and $c_2$ are the slope and constants respectively).
Now let us suppose that point M (-3, 5) is lying on line AD.
So it satisfies the line AD.
$ \Rightarrow 12x - 5y + {c_1} = 0$
$ \Rightarrow 12\left( { - 3} \right) - 5\left( 5 \right) + {c_1} = 0$
$ \Rightarrow {c_1} = 61$
So the equation of line AD is $12x - 5y + 61 = 0$
So the shortest distance between point M and other line $12x - 5y + {c_2} = 0$ is the perpendicular distance so the distance is calculated as
$ \Rightarrow d = \left| {\dfrac{{a{x_1} + b{y_1} + c}}{{\sqrt {{a^2} + {b^2}} }}} \right|$, where a and b are the coefficients of x and y of line and $x_1$ and $y_1$ are the coordinates of point M.
$ \Rightarrow d = \left| {\dfrac{{12\left( { - 3} \right) - 5\left( 5 \right) + {c_2}}}{{\sqrt {{5^2} + {{12}^2}} }}} \right| = \left| {\dfrac{{{c_2} - 61}}{{\sqrt {169} }}} \right| = \left| {\dfrac{{{c_2} - 61}}{{13}}} \right|$
And the distance ($d_2$) between line $5x + 12y - 10 = 0$ and $5x + 12y + 29 = 0$ is given as
\[ \Rightarrow {d_2} = \dfrac{{\left| {{p_1} - {p_2}} \right|}}{{\sqrt {{a^2} + {b^2}} }} = \dfrac{{\left| { - 10 - 29} \right|}}{{\sqrt {{5^2} + {{12}^2}} }} = \dfrac{{\left| { - 39} \right|}}{{13}} = 3\], (where $p_1$ and $p_2$ are the constants of the above equation)
Now both the distances should be equal as they form a square.
$ \Rightarrow \left| {\dfrac{{{c_2} - 61}}{{13}}} \right| = 3$
$ \Rightarrow \left| {{c_2} - 61} \right| = 39$
When modulus opens as positive
$ \Rightarrow + \left( {{c_2} - 61} \right) = 39$
$ \Rightarrow {c_2} = 61 + 39 = 100$
Or, when modulus opens as negative
$ \Rightarrow - \left( {{c_2} - 61} \right) = 39$
$ \Rightarrow {c_2} = 61 - 39 = 22$
So the equation of line BC is $12x - 5y + 22 = 0$ or $12x - 5y + 100 = 0$
As there are two equations possible for line BC therefore there are two squares possible.
Hence option (C) is correct.

Note – Whenever we face such types of question the key concept is the square properties and perpendicular distance formula between two parallel lines and from any point on the line to the another parallel line which is all stated above, so first calculate the equation of perpendicular lines to the given line using that the slope multiplication is equal to (-1) so calculate it as above, then calculate the distance between given parallel lines as above then satisfy the given point on the calculated equation of line so that the constant is calculated then calculate the distance between given point and the opposite parallel line as above then equate both equation and simplify we get two values of constant so the number of square is possible are 2.