Question

Given, 6 blocks of equal mass ‘m’ are placed in the arrangement as shown in the figure. The coefficient of friction between all the blocks are ‘u’ and the ground is smooth find the value of ‘F’ for which tension is >0 for string 2

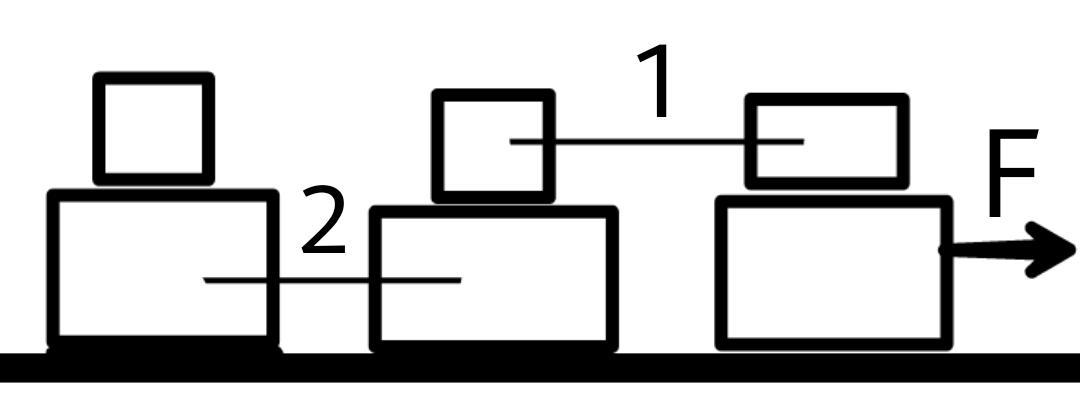
Answer 1

Hint: The important thing is that the tension of strings should not be zero, this is achieved when the block D and E will have the same acceleration and velocity (meaning no relative motion should be present in between the block D and B). This is a case of constrained motion we need to analyse each of the block to find the answer

Complete answer:
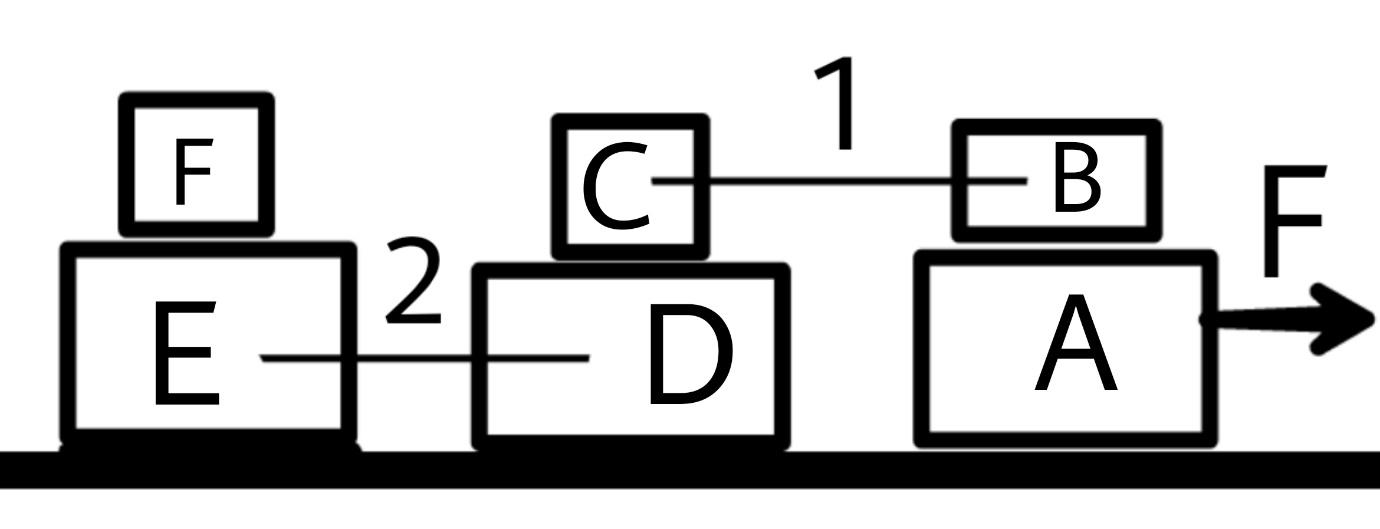
Since all the blocks are in constrained motion their acceleration will be equal.

Now for block E and F.

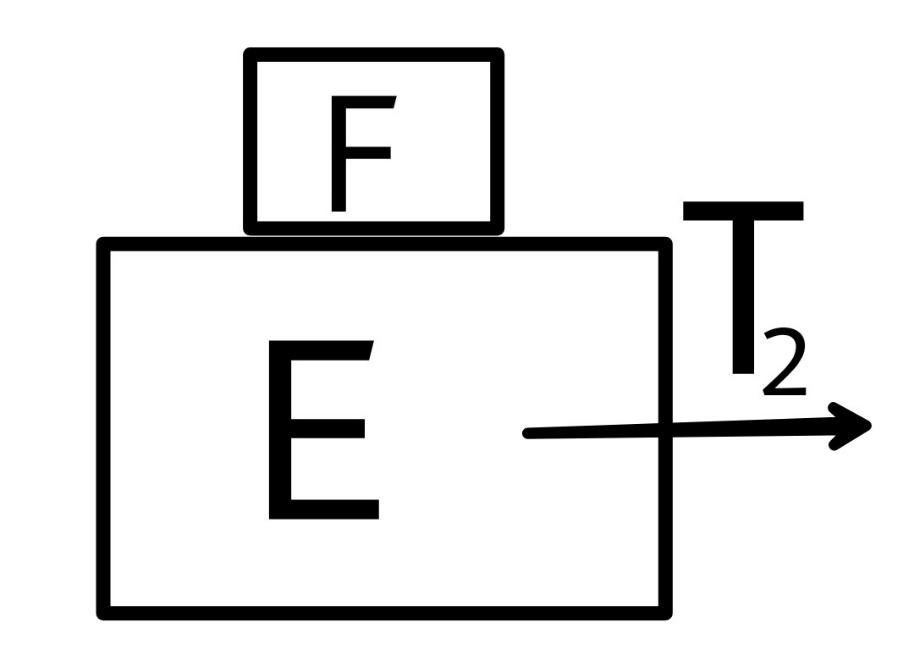
${T_2} = 2ma$
For block C and D

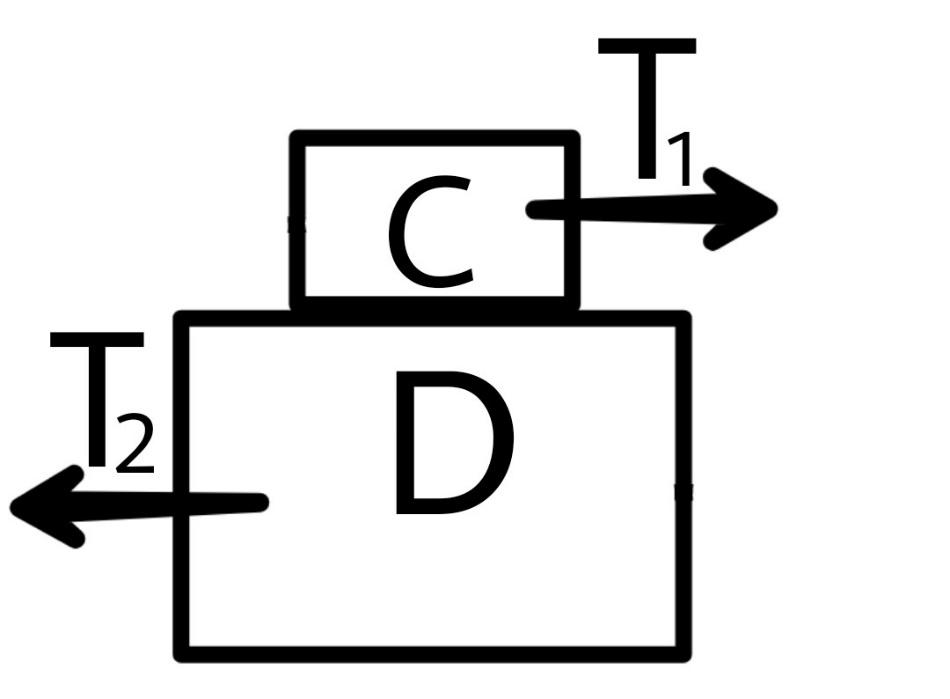
${T_1} - {T_2} = 2ma$
${T_1} = 4ma$
For block A and B

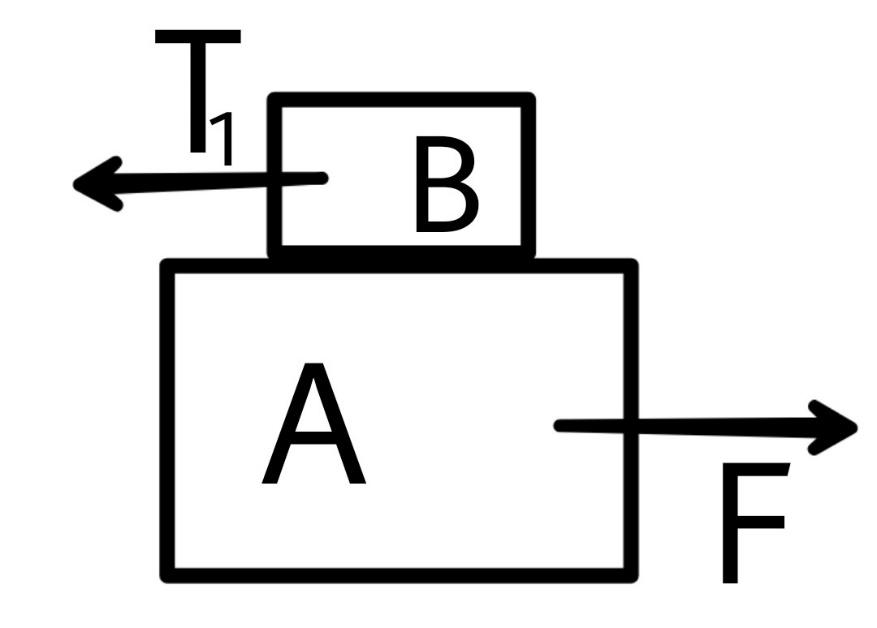
$F - {T_1} = 2ma$
$F = 6ma$
Now the blocks have static friction between them which holds them together. This limits the values of acceleration of the blocks. The range of acceleration becomes
$ma \leqslant \mu mg$
$a \leqslant \mu g$
So, the value of force will become
$F \leqslant 6m\mu g$
So, we can’t increase the value of force more than $6m\mu g$ in order to make the tension in string 2 greater than zero.

Note:
We can further increase the value of force but then there will be slipping between the upper blocks and the lower blocks which will cases the either blocks to move out from each other eventually making the smaller blocks fall from the top of the larger ones this will cause the tension between the two string (both string 1 and string 2) to become zero and only the block A will be moving.