Question

Give the difference between series and parallel connections of resistors.

Answer 1

Hint: When the two or more same electrical devices are used in the same circuit with the energy source, there are two ways to connect the same devices, the devices can be connected by either series or parallel. The series connection means the devices are connected next to the other device in the same wire. But in parallel connection, devices connect with different wires.

Complete step by step answer:
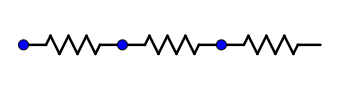
Resistor in series:
When the circuit is connected in the series connection, then the same amount of the current is flowing across all the components in the circuit. Because, the current will have the only one path to flow through the components. For example, let us consider the decoration lights which are used in the functions. In this example, the bulbs are connected in series. In this circuit, all the components are arranged in the same line. The voltage across each resistor is different. If the first resistor has some damage, the whole circuit will break down. There is no flow of voltage or current. The total resistance in the circuit is the sum of the resistance of the individual resistance.
${R_S} = {R_1} + {R_2} + {R_3} + .......$
Where, ${R_S}$ is the total resistance when all the resistors are connected in the series and ${R_1}$, ${R_2}$ are the resistance of the individual resistance.

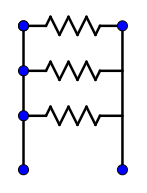
Resistor in parallel:
When the circuit is connected in the parallel connection, then the same amount of voltage is flowing across all the components in the circuit. And the current in the parallel circuit is different because the current will have a different path to flow. In this circuit all the components are arranged in parallel to each other. If any one of the components which are connected in the parallel circuit will get damaged, the other component will work, because every component will have a separate path. The reciprocal of the total resistance is equal to the sum of the reciprocal of the individual resistance.
$\dfrac{1}{{{R_P}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + \dfrac{1}{{{R_3}}}...........$
Where, ${R_P}$ is the total resistance when all the resistors are connected in the parallel and ${R_1}$, ${R_2}$ are the resistance of the individual resistance.

Note:The total voltage in the series connection is equal to the sum of the individual voltages, but in the parallel circuit the voltage across all the components are the same. Then the current in the series circuit is the same across all the components, but in the parallel circuit, the current is the sum of the individual current.