Question

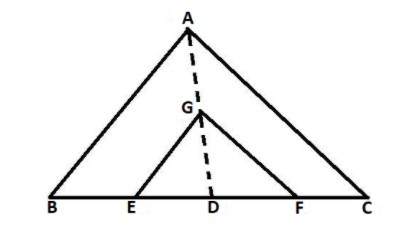
\[G\] is the centroid of $\vartriangle ABC$ . \[GE\] and \[GF\] are drawn parallel to \[AB\] and \[AC\] respectively. Find $A(\vartriangle GEF):A(\vartriangle ABC)$ .

Answer 1

Hint:To solve this question, the property of congruent triangles will be used and then we will infer that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.

Complete step-by-step answer:

In the question, it is given that \[GE\] and \[GF\] are drawn parallel to \[AB\] and \[AC\], respectively. \[G\] is the centroid of $\vartriangle ABC$ .
Now, we will use the corresponding angles theorem which states that if two parallel lines are cut by a transversal, then the pairs of corresponding angles are congruent.
In $\vartriangle ABC$ and $\vartriangle GEF$ ,
\[\angle ABC = \angle GEF\] (Corresponding angles)
\[\angle ACB = \angle GFE\] (Corresponding angles)
Therefore, by AA similarity test, \[\vartriangle {\text{GEF}} \cong \vartriangle {\text{ABC}}\] .

We know that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
Therefore, \[\dfrac{{\vartriangle {\text{GEF}}}}{{\vartriangle {\text{ABC}}}} = \dfrac{{G{D^2}}}{{A{D^2}}}\]
Now, we know that the centroid divides the median in the ratio \[2:1\] .
Therefore, \[AG:GD = 2:1\]
So, \[AD:GD = 3:1\]
Or, \[GD:AD = 1:3\]
Therefore, \[\dfrac{{\vartriangle {\text{GEF}}}}{{\vartriangle {\text{ABC}}}} = \dfrac{{G{D^2}}}{{A{D^2}}} = \dfrac{{{1^2}}}{{{3^2}}} = \dfrac{1}{9}\]
Hence, $A(\vartriangle GEF):A(\vartriangle ABC) = 1:9$

Note:To solve such type of geometry questions, you need to remember the properties of triangle. Remember that the centroid of a triangle is the intersection of the three medians of the triangle (each median connecting a vertex with the midpoint of the opposite side). Also, AA Similarity Postulate states that if two angles in one triangle are congruent to two angles in another triangle, the two triangles are similar.