Question

A circular park of radius 20 m is situated in a colony. Three boys Ankur, Syed and David are sitting at equal distance on its boundary each having a toy telephone in their hands to talk to each other. Find the length of string of each phone?

Answer 1

Hint: First of all draw the figure as per the information given in the question. It is given that the three boys are sitting at equal distance from each other and they are holding a toy telephone and are talking to each other. We have to find the length of the string. The three boys when talking to each other using a toy telephone then the 3 strings are making an equilateral triangle and the length of the string is equal to the side of the equilateral triangle so using geometry we can find the side of the equilateral triangle.

Complete step-by-step answer:
In the below figure, we have shown a circular park with radius r in which three boys are sitting at equal distance with strings represented by BC, CD and BD
 

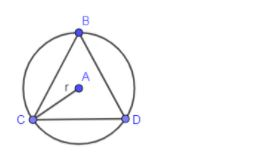
We have to find the length of each string which we are going to find by calculating the side of this equilateral $\Delta BCD$.
In equilateral triangle, all the angles are of ${{60}^{\circ }}$ so $\angle ACD={{30}^{\circ }}$. In the below diagram, we have modified the above diagram so that calculations will be easy.

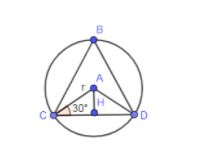
The radius of the circular park is given as 20 m. We are going to find the side of the equilateral triangle CD using the above diagram.
In $\Delta ACH$, using trigonometric ratio $\cos {{30}^{\circ }}$ we can find the length CH.
We know that,
$\cos {{30}^{\circ }}=\dfrac{B}{H}$
In the above equation, “B” stands for the base of the triangle and “H” stands for hypotenuse of the triangle with respect to angle ${{30}^{\circ }}$. From the above diagram, the base is CH and the hypotenuse is AC.
$\cos {{30}^{\circ }}=\dfrac{CH}{AC}$
Now, AC is the radius of the circular park so substituting the value of AC as 20 m in the above equation we get,
$\cos {{30}^{\circ }}=\dfrac{CH}{20}$
We also know that the value of $\cos {{30}^{\circ }}=\dfrac{\sqrt{3}}{2}$ so substituting this value in the above equation we get,
$\dfrac{\sqrt{3}}{2}=\dfrac{CH}{20}$
As you can see that denominators of L.H.S and R.H.S are divisible by 2 so dividing the denominator by 2 on both the sides of the above equation we get,
$\dfrac{\sqrt{3}}{1}=\dfrac{CH}{10}$
On cross multiplying the above equation we get,
$10\sqrt{3}=\text{CH}$
Now, CH = HD so double the value of CH will give the value of side CD,
$20\sqrt{3}=2\left( CH \right)=CD$
From the above calculations, we have found the side of the equilateral triangle as $20\sqrt{3}$.
Hence, the length of each string is equal to $20\sqrt{3}$.

Note: You might have thought that path of the string lies on the circumference of the circular park but you should imagine the practical situation imagine you and you friend are on the boundary of the circular park and are holding a toy telephone then the string between you and your friend is in the straight line not in the shape of arc of the circle.
In the above solution, we have shown that CH = HD in the following figure:

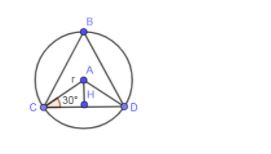
We are going to prove how CH = HD.
In $\Delta AHD$,
AD is equal to r and $\angle ADH={{30}^{\circ }}$so similarly as we have found the side CH in the above solution using $\cos {{30}^{\circ }}$ we can find the side HD.
$\cos {{30}^{\circ }}=\dfrac{HD}{AD}$
Substituting the value of $\cos {{30}^{\circ }}$and the value of AD as 20 m in the above equation we get,
$\dfrac{\sqrt{3}}{2}=\dfrac{HD}{20}$
On cross multiplying we get,
$20\sqrt{3}=2\left( HD \right)$
Dividing 2 on both the sides we get,
$10\sqrt{3}=HD$
In the above solution, we have got the value of CH as the same as HD.
Hence, we have shown CH = HD.