Question

From the top of a hill, the angles of depression of two consecutive kilometer stones due east are found to be ${{30}^{\circ }}$ and ${{45}^{\circ }}$. Find the height of the hill.
(a) 1.365 km
(b) 1.5 km
(c) 1.7 km
(d) 1.1 km

Answer 1

Hint:Assume the height of the hill be $h$ km and distance between the foot of the hill and first stone be $x$ km. Use tangent of given angles, that is, $\tan \theta =\dfrac{\text{perpendicular}}{\text{base}}$ to obtain two equations for two variables, $x\text{ and }h$ and solve them to find the height.

Complete step-by-step answer:
The term angle of depression denotes the angle from the horizontal downward to an object. An observer’s line of sight would be below the horizontal. The angle of elevation and the angle of depression are congruent.
Now, we come to the question. We have been given two consecutive kilometer stones, that means the distance between the two stones is 1 km. Let us assume that the height of the hill is $h$ km. Now, when we will imagine how the system of observer, stones and hill will look, we will see that it will form two right angle triangles. Let stone 1 be at C and stone 2 at D. AB is the hill.

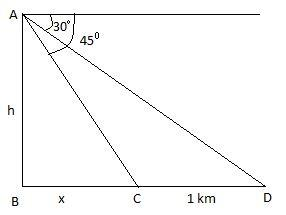
We know that \[\tan \theta =\dfrac{\text{perpendicular}}{\text{base}}....................(i)\]
Using relation (i), in triangle ABC we get,
$\tan {{45}^{\circ }}=\dfrac{BC}{AB}=\dfrac{x}{h}$
We know that $\tan {{45}^{\circ }}=1$,
$\begin{align}
  & \therefore \dfrac{x}{h}=1 \\
 & x=h.....................(ii) \\
\end{align}$
Now, using relation (i), in triangle ABD we get,
$\tan {{60}^{\circ }}=\dfrac{x+1}{h}$
We know that $\tan {{60}^{\circ }}=\sqrt{3}$,
$\begin{align}
  & \therefore \sqrt{3}=\dfrac{x+1}{h} \\
 & \sqrt{3}h=x+1.........................(iii) \\
\end{align}$
Therefore, using equations (i) and (iii), we get,
$\begin{align}
  & \sqrt{3}h=h+1 \\
 & \sqrt{3}h-h=1 \\
 & h\left( \sqrt{3}-1 \right)=1 \\
 & h=\dfrac{1}{\left( \sqrt{3}-1 \right)} \\
\end{align}$
Now, rationalizing the denominator, we get,
$\begin{align}
  & h=\dfrac{1}{\left( \sqrt{3}-1 \right)}\times \dfrac{\left( \sqrt{3}+1 \right)}{\left( \sqrt{3}+1 \right)} \\
 & =\dfrac{\left( \sqrt{3}+1 \right)}{3-1} \\
 & =\dfrac{\left( \sqrt{3}+1 \right)}{2} \\
 & =\dfrac{1.73+1}{2} \\
 & =1.365 \\
\end{align}$
Hence, the height of the hill is 1.365 km. Therefore, option (a) is the correct answer.

Note: We have used $\sqrt{3}=1.73$. As we can see that angle of depressions are ${{45}^{\circ }}\text{ and 3}{{\text{0}}^{\circ }}$. Therefore, in right angle triangle ABC $\angle CAB={{90}^{\circ }}-{{45}^{\circ }}$= ${{45}^{\circ }}$ and in triangle ABD $\angle DAB={{90}^{\circ }}-{{30}^{\circ }}$= ${{60}^{\circ }}$. We have rationalized the denominator to make our calculation easy.Students should remember the important trigonometric identities and trigonometric ratios for solving these types of questions.