Question

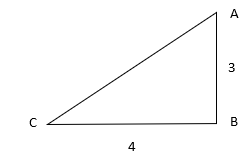
From the following figure find the value of $\sin C$?

${\text{(A) }}\dfrac{{\text{2}}}{{\text{3}}}$
${\text{(B) }}\dfrac{3}{5}$
${\text{(C) }}\dfrac{{\text{2}}}{7}$
${\text{(D) }}\dfrac{6}{5}$

Answer 1

Hint: Here we have to find the value of ${\text{sin C}}$. First we will first find the length of the hypotenuse of the triangle and then calculate the value of ${\text{sin C}}$ by using the formula. Finally we get the required answer.

Formula used: Pythagoras theorem: ${a^2} + {b^2} = {c^2}$, where $a,b$ and $c$ are lengths of the triangle $\vartriangle ABC$ respectively.
$\sin \theta = \dfrac{{opposite}}{{hypotenuse}}$

Complete step-by-step solution:
From the diagram we can see that $\vartriangle ABC$ is a right-angled triangle which has sides $AB,BC$ and $AC$.
The length of side $AB$ from the diagram is $3$ therefore:
$AB = 3$.
The length of side $BC$ from the diagram is $4$ therefore:
$BC = 4$.
Now we will find the length of the missing side using Pythagoras theorem.
Since$\vartriangle ABC$ is a right-angled triangle we know that:
${(AC)^2} = {(AB)^2} + {(BC)^2}$
On substituting the values, we get:
$\Rightarrow$${(AC)^2} = {(3)^2} + {(4)^2}$
This could be expanded as:
$\Rightarrow$${(AC)^2} = 9 + 16$
On further simplifying we get:
$\Rightarrow$${(AC)^2} = 25$
This could be also written as:
$\Rightarrow$${(AC)^2} = {(5)^2}$
Since there is a square on both sides, we take the square root of both sides.
$\Rightarrow$$AC = 5$
Now we have to find the value of $\sin C$,
${\text{sin C = }}\dfrac{{{\text{opposite}}}}{{{\text{hypotenuse}}}}$
The side opposite to angle $C$ is the side $AB$
Therefore, $\sin C = \dfrac{{AB}}{{AC}}$
On substituting the values, we get:
$\Rightarrow$$\sin C = \dfrac{3}{5}$

Therefore, the correct option is $(B)$ which is $\dfrac{3}{5}$.

Note: It exists $\cos \theta = \dfrac{{adjacent}}{{hypotenuse}}$ where the adjacent side is the side which is next to the angle; it is also called the perpendicular side.
Example: $\cos C = \dfrac{{BC}}{{AC}}$
Also, there is $\tan \theta = \dfrac{{\sin \theta }}{{\cos \theta }} = \dfrac{{opposite}}{{adjacent}}$
Example: $\tan C = \dfrac{{AB}}{{BC}}$
There also exist other trigonometric relations which are $\sec \theta $ $\cos ec\theta $ and $\cot \theta $ which are the inverse of $\cos \theta ,\sin \theta $ and $\tan \theta $ respectively.
In this question, we had to find $\sin C$ therefore, the opposite side to the angle $C$ was side $AB$.
If it was asked to find out $\sin A$ then the opposite side to the angle $A$ is $BC$ which is the base of the triangle.
These $6$ are the trigonometric relations which are present in trigonometry.