Question

From point P, \[10\] cm away from the centre of a circle, a tangent PT of length\[\;8\] cm is drawn. Find the radius of the circle.

Answer 1

Hint: Form a right angle triangle, by joining the end with point T to the centre of the circle. Then use Pythagoras theorem which states that, “In a right angled triangle, the sum of the square of the hypotenuse side is equal to the sum of squares of the two other sides.” This can also be written as-
${H^2} = {P^2} + {B^2}$ Where H is the hypotenuse, P is the perpendicular of the triangle and B is the Base of the Triangle. Put the values to find the radius.

Complete step-by-step answer:
Given, Point P is \[10\]cm away from the centre of a circle and a tangent is drawn from this point of length \[\;8\] cm named PT.
We have to find the radius of the circle.

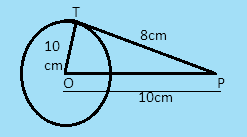
Let O be the centre of the given circle and P be such a point that OP=\[10\]cm
Then PT is the tangent with length=\[\;8\] cm
Now Join OT to form a triangle. Here OT is the radius of the circle through T. Then we can say that OT$ \bot $ PT which means $\vartriangle OTP$ is a right angled triangle.
Then by Pythagoras theorem, we get-
 $ \Rightarrow $ ${H^2} = {P^2} + {B^2}$ Where H is the hypotenuse, P is the perpendicular of the triangle and B is the Base of the Triangle
Here, OP is the hypotenuse, PT is the base and OT is the perpendicular,
$ \Rightarrow O{P^2} = O{T^2} + P{T^2}$
Then we can write it as-
\[ \Rightarrow O{T^2} = O{P^2} - P{T^2}\]
On putting the values we get,
\[ \Rightarrow O{T^2} = {10^2} - {8^2}\]
On solving we get,
\[ \Rightarrow O{T^2} = 100 - 64 = 36\]
On simplifying we get,
\[ \Rightarrow OT = \sqrt {36} = 6\] cm

The radius of the circle is $6$cm.

Note: Here the student may go wrong if they assume that OT is perpendicular on OP because then PT will become hypotenuse, OT will become perpendicular and OP will become base. If these values are put in the Pythagoras theorem then the value of radius will be $6i$ which is not possible. Hence correctly draw the diagram so as not to get confused which is the right angle in the formed triangle.