Question

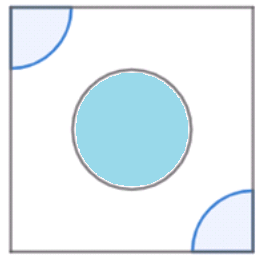
From each of the two opposite corners of a square of side 8 cm, a quadrant of a circle of radius 1.4 cm is cut. Another circle of radius 4.2 cm is also cut from the centre as shown in the figure. Find the area of the remaining portion of the square. (Use \[\pi =\dfrac{22}{7}\] ).

Answer 1

Hint: In this question, we first need to look into the diagram and then be clear about what we have to find. Calculate the area of the square, area of the circle and the area of the quadrant of the circle. Then find the appropriate relation between these areas to get the required area.

Complete step-by-step solution -
Let us look at the definitions and the formulae.
In geometry, a square is a regular quadrilateral, which means it has four equal sides and four equal angles. It can also be defined as a rectangle in which two adjacent sides have equal length.
Area of a square with side length is given by:
\[s\times s={{s}^{2}}\]
Circle: A circle is a set of points which lie in a plane and at a constant distance from a fixed point in the plane.
Radius: Radius is the shortest distance between the centre of the circle and a point on the circumference of the circle.
Area of a circle with radius r is given by:
\[\pi {{r}^{2}}\]
Quadrant of a circle: One -fourth section of a circle when the circle is divided evenly into four parts is called the quadrant of a circle.
Area of quadrant of a circle of radius r is given by:
\[\dfrac{1}{4}\pi {{r}^{2}}\]

Now, from the given conditions
Let us assume the area of square as A1, area of circle as A2, area of the quadrant as A3.
Also side length of the square as s, radius of the circle as r1, radius of the quadrant of the circle as r2.
Given,
\[s=8,{{r}_{1}}=4.2,{{r}_{2}}=1.4\]
Now, let us calculate the areas of the respective figures.
\[\begin{align}
  & \Rightarrow {{A}_{1}}={{s}^{2}} \\
 & \Rightarrow {{A}_{1}}={{8}^{2}} \\
 & \therefore {{A}_{1}}=64c{{m}^{2}} \\
\end{align}\]
\[\begin{align}
  & \Rightarrow {{A}_{2}}=\pi {{r}_{1}}^{2} \\
 & \Rightarrow {{A}_{2}}=\pi {{\left( 4.2 \right)}^{2}} \\
 & \Rightarrow {{A}_{2}}=\pi \times 17.64 \\
 & \Rightarrow {{A}_{2}}=\dfrac{22}{7}\times 17.64\text{ }\left[ \because \pi =\dfrac{22}{7} \right] \\
\end{align}\]
\[\begin{align}
  & \Rightarrow {{A}_{2}}=22\times 2.52 \\
 & \therefore {{A}_{2}}=55.44c{{m}^{2}} \\
\end{align}\]
\[\begin{align}
  & \Rightarrow {{A}_{3}}=\dfrac{1}{4}\pi {{r}_{2}}^{2} \\
 & \Rightarrow {{A}_{3}}=\dfrac{1}{4}\pi {{\left( 1.4 \right)}^{2}} \\
 & \Rightarrow {{A}_{3}}=\dfrac{1}{4}\pi \times 1.96 \\
\end{align}\]
\[\begin{align}
  & \Rightarrow {{A}_{3}}=\dfrac{1}{4}\times \dfrac{22}{7}\times 1.96\text{ }\left[ \because \pi =\dfrac{22}{7} \right] \\
 & \Rightarrow {{A}_{3}}=\dfrac{1}{4}\times 22\times 0.28 \\
\end{align}\]
\[\therefore {{A}_{3}}=1.54c{{m}^{2}}\]
Now, the area of the remaining portion can be calculated by subtracting the area of the circle and area of two quadrants of the circle from the area of the square.
Let us assume that the area of the remaining portion as A.
\[\begin{align}
  & \Rightarrow A={{A}_{1}}-{{A}_{2}}-2{{A}_{3}} \\
 & \Rightarrow A=64-55.44-\left( 2\times 1.54 \right) \\
 & \Rightarrow A=64-55.44-3.08 \\
 & \Rightarrow A=64-\left( 55.44+3.08 \right) \\
 & \Rightarrow A=64-58.52 \\
 & \therefore A=5.48c{{m}^{2}} \\
\end{align}\]
Hence, the area of the remaining portion is 5.48 square cm.

Note: As the given figure is symmetric we can also find the area of the remaining portion by considering only half of the given figure. Then calculate the area of the semi circle , area of the quadrant and the area of the triangle formed with the diagonal of the square as base. The area of the remaining portion will be twice the subtraction of the area of the semi circle and the area of the quadrant of the circle from the area of the triangle formed with the diagonal of the square as base. Both the methods give the same result.
It is important to note that while solving the question we need to substitute the corresponding values of the radius in the area formula of the circle and quadrant of the circle because interchanging those values changes the result completely.